写在前面
- 记录日常刷题,不间断更新…
数组
二分查找
解法一:暴力
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int search(vector<int> &nums, int target) {
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == target) {
return i;
}
}
return -1;
}
}解法二:二分法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
int search(vector<int> &nums, int target) {
int left, right, middle;
left = 0;
right = nums.size() - 1;
middle = (left + right) / 2;
int i = 1;
// 这里一定要是left <= right 不能是left < right
while (left <= right) {
if (nums[middle] < target) {
left = middle + 1;
middle = (left + right) / 2;
} else if (nums[middle] > target) {
right = middle - 1;
middle = (left + right) / 2;
} else {
return middle;
}
}
return -1;
}
};
移除元素
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int removeElement(vector<int> &nums, int val) {
int cnt = 0;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == val) {
cnt++;
} else {
nums[i - cnt] = nums[i];
}
}
return nums.size() - cnt;
}
}
有序数组的平方
解法一:
1
2
3
4
5
6
7
8
9
10class Solution {
public:
vector<int> sortedSquares(vector<int> &nums) {
for (int i = 0; i < nums.size(); ++i) {
nums[i] *= nums[i];
}
sort(nums.begin(), nums.end()); // 快速排序 会占用(logn)额外空间
return nums;
}
};解法二:双指针向中间移动,从最大值开始构建结果数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<int> sortedSquares(vector<int> &nums) {
int n = nums.size() - 1;
vector<int> res(nums.size(), 0);
for (int i = 0, j = n; i <= j;) {
if (nums[i] * nums[i] < nums[j] * nums[j]) {
res[n--] = nums[j] * nums[j];
j--;
} else {
res[n--] = nums[i] * nums[i];
i++;
}
}
return res;
}
};解法三:双指针。先找到“零点”
neg,即最接近0的点。左指针=neg,右指针=neg+1,向两端移动,从最小值开始构建结果数组1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
vector<int> sortedSquares(vector<int> &nums) {
int n = nums.size();
int negative = -1;
for (int i = 0; i < n; ++i) {
if (nums[i] < 0) {
negative = i;
} else {
break;
}
}
vector<int> ans;
int i = negative, j = negative + 1;
while (i >= 0 || j < n) {
if (i < 0) {
ans.push_back(nums[j] * nums[j]);
++j;
} else if (j == n) {
ans.push_back(nums[i] * nums[i]);
--i;
} else if (nums[i] * nums[i] < nums[j] * nums[j]) {
ans.push_back(nums[i] * nums[i]);
--i;
} else {
ans.push_back(nums[j] * nums[j]);
++j;
}
}
return ans;
}
};
长度最小的子数组
解法一:暴力,两层循环,每次找到符合条件的位置,更新
s值并退出1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int minSubArrayLen(int s, vector<int> &nums) {
int result = nums.size() + 1;
for (int i = 0; i < nums.size(); ++i) {
int sum = 0;
for (int j = i; j < nums.size(); ++j) {
sum += nums[j];
if (sum >= s) {
result = result < (j - i + 1) ? result : (j - i + 1);
break;
}
}
}
return res == nums.size() + 1 ? 0 : res;
}
};解法二:滑动窗口,
i代表窗口左值,j代表窗口右值,当sum >= s代表应该缩小窗口了,先更新s值再更新窗口总值sum,最后更新窗口左值,即将窗口左边框右移一格1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int minSubArrayLen(int s, vector<int> &nums) {
int sum = 0;
int res = nums.size() + 1;
int i = 0;
for (int j = 0; j < nums.size(); ++j) {
sum += nums[j];
while (sum >= s) { // 应该缩小窗口啦
res = res < (j - i + 1) ? res : (j - i + 1); // 更新s值
sum = sum - nums[i]; // 窗口缩小了,窗口总值也要变(小)
i++; // 窗口左边右移一格,窗口缩小
}
}
return res == nums.size() + 1 ? 0 : res;
}
};
水果成篮
解法一:暴力失败,70/90测试用例给了40000个0,直接超时了哈哈哈哈哈,下面贴出我的
Junk Code1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
int totalFruit(vector<int> &fruits) {
int res = 1;
int left = -1;
for (int i = 0; i < fruits.size() - 1; ++i) {
int sum = 1;
left = fruits[i];
int right = -1;
for (int j = i + 1; j < fruits.size(); ++j) {
if (fruits[j] == left) {
sum++;
} else if (right == -1) {
right = fruits[j];
sum++;
} else if (fruits[j] == right) {
sum++;
} else {
res = res > sum ? res : sum;
break;
}
res = res > sum ? res : sum;
}
}
return res;
}
};解法二:滑动窗口。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52class Solution {
public:
int totalFruit(vector<int> &fruits) {
int res = 0; // 最终结果
int basket1 = fruits[0]; // 一号篮子,直接初始化
int basket2 = -1; // 二号篮子
int index1 = 0; // 记录最新放入一号篮子的水果的下标
int index2 = 0; // 记录最新放入二号篮子的水果的下标
int cnt = 0; // 记录每一次水果种类发生变化后,两个篮子装入水果的总数
// 遍历,依次比较每个当前的水果种类 和篮子中的水果种类是否一样,一样则可以放入,不一样则重新分配篮子
for (int i = 0; i < fruits.size(); ++i) {
// 当前水果可以放入一号篮子,更新下标和数量
if (basket1 == fruits[i]) {
++cnt;
index1 = i;
}
// 当前水果种类和一号篮子已有水果种类不一致,比较二号篮子
// 二号篮子没有水果,直接放入
else if (basket2 == -1) {
++cnt;
index2 = i;
basket2 = fruits[i];
}
// 二号篮子有水果,且种类一致,可以放进
else if (basket2 == fruits[i]) {
index2 = i;
++cnt;
}
// 当前水果不能放入篮子 需要重新分配
// 找到最久没有放入水果的篮子,更新该篮子里的水果种类,以及最新放入水果的下标,和已放入篮子里水果的数量
else {
if (index1 < index2) {
cnt = i - index1;
basket1 = fruits[i];
index1 = i;
} else {
cnt = i - index2;
basket2 = fruits[i];
index2 = i;
}
}
res = res > cnt ? res : cnt;
}
return res;
}
};
螺旋矩阵
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
public:
vector<int> spiralOrder(vector<vector<int>> &matrix) {
if (matrix.empty()) {
return {};
}
vector<int> res;
int col = matrix.size();
int row = matrix[0].size();
int up = 0;
int down = col - 1;
int left = 0;
int right = row - 1;
while (true) {
for (int i = left; i <= right; ++i) {
res.push_back(matrix[up][i]);
}
// 上面一行遍历结束,上边界加一,若大于下边界,代表遍历完成
if (++up > down) break;
for (int i = up; i <= down; ++i) {
res.push_back(matrix[i][right]);
}
// 右边一列遍历结束,右边界加一,若右边界小于左边界,代表遍历完成
if (--right < left) break;
for (int i = right; i >= left; --i) {
res.push_back(matrix[down][i]);
}
if (--down < up) break;
for (int i = down; i >= up; --i) {
res.push_back(matrix[i][left]);
}
if (++left > right) break;
}
return res;
}
};
解法二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
vector<int> spiralOrder(vector<vector<int>> &matrix) {
vector<int> res;
int col = matrix.size();
int row = matrix[0].size();
int top = 0;
int bottom = col - 1;
int left = 0;
int right = row - 1;
int cnt = 1; // 记录已经处理了多少个数
while (true) {
// 遍历第top行,每向res中添加一个数,都要进行判断是否已添加完
for (int i = left; i <= right; ++i) {
res.push_back(matrix[top][i]);
++cnt;
if (cnt > col * row) return res;
}
++top; // 更新边界值
for (int i = top; i <= bottom; ++i) {
res.push_back(matrix[i][right]);
++cnt;
if (cnt > col * row) return res;
}
--right;
for (int i = right; i >= left; --i) {
res.push_back(matrix[bottom][i]);
++cnt;
if (cnt > col * row) return res;
}
--bottom;
for (int i = bottom; i >= top; --i) {
res.push_back(matrix[i][left]);
++cnt;
if (cnt > col * row) return res;
}
++left;
}
}
};
螺旋矩阵Ⅱ
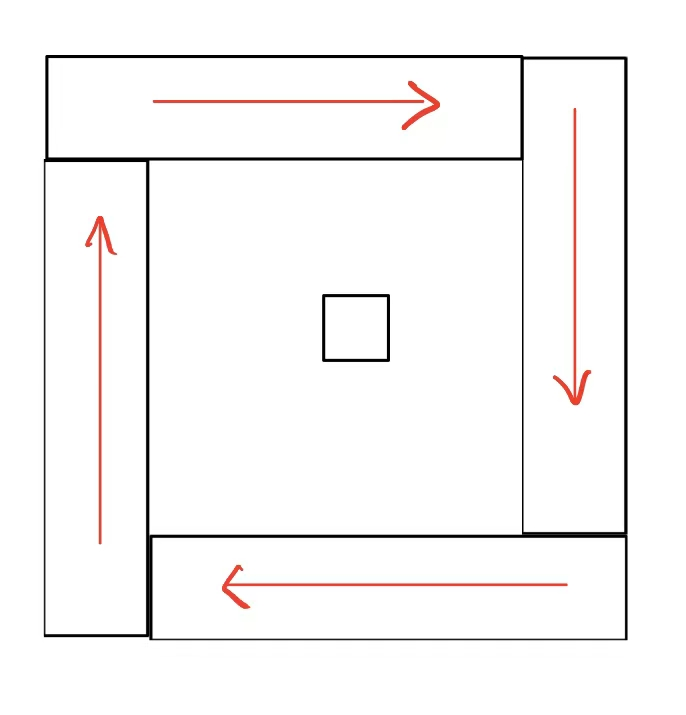
解法一:当n为奇数时,最中间的点得不到填充,需要额外处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0));
int loop = n / 2;
int startX = 0;
int startY = 0;
int offset = 1;
int cnt = 1;
int i, j;
int border = n - offset;
while (loop--) {
i = startX;
j = startY;
for (j = startY; j < border; ++j) {
res[i][j] = cnt++;
}
for (i = startX; i < border; ++i) {
res[i][j] = cnt++;
}
for (; j > startY ; --j) {
res[i][j] = cnt++;
}
for (; i > startX; --i) {
res[i][j] = cnt++;
}
startX++;
startY++;
border++;
offset += 2;
}
if (n % 2 != 0) {
res[n / 2][n / 2] = cnt;
}
return res;
}
};
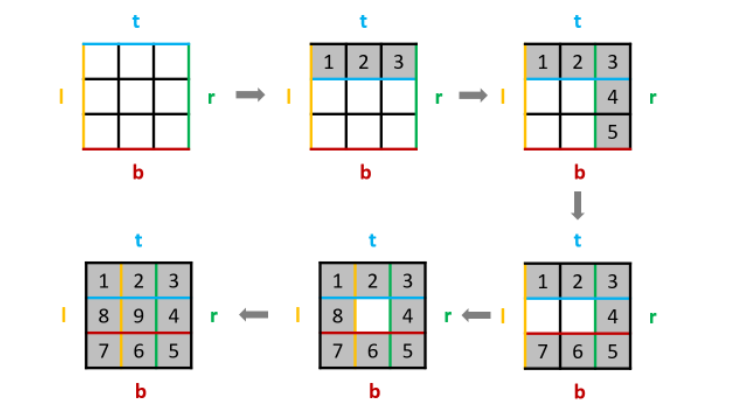
解法二:修改了方法一的缺陷,代码更简洁,参考链接
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0));
int left = 0, right = n - 1, top = 0, bottom = n - 1;
int cnt = 1;
while (cnt <= n * n) {
for (int i = left; i <= right; ++i) {
res[top][i] = cnt++;
}
++top;
for (int i = top; i <= bottom; ++i) {
res[i][right] = cnt++;
}
--right;
for (int i = right; i >= left; --i) {
res[bottom][i] = cnt++;
}
--bottom;
for (int i = bottom; i >= top; --i) {
res[i][left] = cnt++;
}
++left;
}
return res;
}
};
链表
移除链表元素
解法一:迭代。由于头结点可能被删除,我们创建一个新的头节点
newHead,初始化使得newHead->next = head,处理完成后,返回newHead->next。temp代表当前节点,如果当前节点的下一个节点不为空,并且下一个节点的值为val,则删除下一个节点。如果下一个节点的值不等于val,则保留,并让temp指向下一个节点。若下一个节点为空,则遍历结束。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
ListNode *removeElements(ListNode *head, int val) {
ListNode *newHead = new ListNode(0, head);
ListNode *temp = newHead;
while (temp->next) {
if (temp->next->val == val) {
temp->next = temp->next->next;
} else {
temp = temp->next;
}
}
return newHead->next;
}
};
解法二:先处理头结点,再处理后续节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
ListNode* removeElements(ListNode* head, int val) {
if (head == nullptr || val == 0){
return head;
}
// 处理头结点
while (head != nullptr && head->val == val) {
head = head->next;
}
// 处理剩下节点
ListNode* cur = head;
while (cur != nullptr && cur->next != nullptr){
if (cur->next->val == val){
cur->next = cur->next->next;
}else {
cur = cur->next;
}
}
return head;
}
};
设计链表
初始化链表时,初始化一个虚拟节点,这样方便后续处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84class MyLinkedList {
public:
struct LinkedNode {
int val;
LinkedNode* next;
LinkedNode(int val):val(val), next(nullptr){}
};
// 初始化一个虚拟节点作为头结点,size记录链表长度
MyLinkedList() {
dummy = new LinkedNode(0);
size = 0;
}
int get(int index) {
if (index < 0 || index >= size){
return -1;
}
LinkedNode* cur = dummy->next;
while (index--){
cur = cur->next;
}
return cur->val;
}
void addAtHead(int val) {
LinkedNode* temp= new LinkedNode(val);
temp->next = dummy->next;
dummy->next = temp;
size++;
}
void addAtTail(int val) {
LinkedNode* cur = dummy;
while (cur->next != nullptr){
cur = cur->next;
}
LinkedNode* temp= new LinkedNode(val);
cur->next = temp;
size++;
}
void addAtIndex(int index, int val) {
if (index > size){
return;
}else{
LinkedNode* temp = new LinkedNode(val);
if(index < 0){
addAtHead(val);
size++;
}else{
LinkedNode* cur = dummy;
while(index--){
cur = cur->next;
}
temp->next = cur->next;
cur->next = temp;
size++;
}
}
}
void deleteAtIndex(int index) {
if (index < 0 || index >= size){
return;
}
if (index == 0){
dummy->next = dummy->next->next;
size--;
return;
}
LinkedNode* cur = dummy->next;
index--; // 这里先减一,后续找到的节点就是目标节点的前一个节点,这样方便进行删除操作
while(index--){
cur = cur->next;
}
cur->next = cur->next->next;
size--;
}
private:
int size;
LinkedNode *dummy;
};
反转链表
解法一:定义一个新链表,遍历原始链表,将原始链表中的每个节点采用头插法的方式,插入新链表中。这种方法会浪费内存。
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* newList = new ListNode;
while(head != nullptr){
ListNode* temp = new ListNode;
temp->val = head->val;
temp->next = newList->next;
newList->next = temp;
head = head->next;
}
return newList->next;
}
解法二:
pre用来记录上一个访问的节点,next用来保存下一个节点1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* next = nullptr;
while (head != nullptr) {
next = head->next; // 保存下一个节点
head->next = pre; // 将节点的指针指向上一个节点
pre = head; // 更新pre
head = next; // 更新head
}
return pre; // 注意这里返回的是pre,因为处理完尾结点之后,pre存储的是尾结点,但head存储的是个空节点!!
}
};
解法三:递归
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
ListNode* reverse(ListNode* pre,ListNode* cur){
if (cur == NULL) return pre;
ListNode* temp = cur->next; // 更新当前节点
cur->next = pre; // 当前节点指向前节点
return reverse(cur, temp); // 传入前指针和当前节点
}
ListNode* reverseList(ListNode* head) {
return reverse(NULL, head); // 传入前指针和当前节点
}
};
两两交换链表中的节点
使用虚拟头结点比较方便处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* virtualHead = new ListNode;
virtualHead->next = head;
ListNode* cur = virtualHead;
while(cur->next != nullptr && cur->next->next != nullptr){
ListNode* thisNode = cur->next; // 保存临时节点
ListNode* nextNode = cur->next->next->next; // 保存临时节点
// 开始交换
cur->next = cur->next->next;
cur->next->next = thisNode;
cur->next->next->next = nextNode;
// 交换完成 更新cur位置
cur = cur->next->next;
}
return virtualHead->next;
}
};
func swapPairs(head *ListNode) *ListNode {
dummyNode := &ListNode{Val: 0}
dummyNode.Next = head
cur := head // 指向 欲交换节点对 的第一个节点, 比如a,b,c,d要交换节点b,c, 那么cur就指向节点b
pre := dummyNode // 指向 欲交换节点对 的上一个节点, 比如a,b,c,d要交换节点b,c, 那么pre就指向节点b的上一个节点, 也就是节点a
// 用 a->b->c->d->e->...举例, 将要交换b,c
// 此时 cur指向b, pre指向a
for cur != nil && cur.Next != nil {
next := cur.Next.Next // ① next指向d
pre.Next = cur.Next // ② pre后接节点c, a->c->d->e->... b->c
cur.Next.Next = cur // ③ 更新cur节点, 指向节点b, a->b<->c d->e->...
cur.Next = next // ④ b后接节点d, a->c->b->d->e->...
pre = cur // ⑤ pre更新为b
cur = next // ⑥ cur更新为d
}
return dummyNode.Next
}这道题有了思路自己模拟一下,很好就写出来了。
删除链表的倒数第 N 个结点
解法一:先遍历一遍,计算出链表长度,定位到目标节点的前一个位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
int size = 0;
ListNode* virtualHead = new ListNode;
virtualHead->next = head;
ListNode* cur = virtualHead;
while(cur->next != nullptr){
cur = cur->next;
size++;
}
if (n == size){ // 要删除的节点就是第一个节点,直接返回,避免21行处理出错
return head->next;
}
int index = size - n;
cur = virtualHead;
while(index--){
cur = cur->next;
}
cur->next = cur->next->next;
return head;
}
};
解法二:倒数第n个就是正数第
m-n+1个,为了方便删除,找到目标节点的前一个位置,即m-n处。采用双指针fast和slow。fast先行n+1个单位距离,此时slow再从起点出发,与fast始终保持n+1个距离。当fast到达尾结点时,slow位于倒数第n+1个节点处1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* virtualHead = new ListNode;
virtualHead->next = head;
ListNode* fast = new ListNode;
ListNode* slow = new ListNode;
int temp = n+1;
fast = virtualHead;
while(temp--){
fast = fast->next;
}
slow = virtualHead;
while(fast!=nullptr){
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
return virtualHead->next;
}
};
链表相交
注意,题里说的相等指的是节点的地址相等,而不是值相等(地址相等了,值肯定相等,但是值相等,地址不一定相等)。换个说法,所谓找到起始节点,其实就是找到两个链表的公共节点。
思路分析:将两个链表进行”尾部对齐”,因为若存在公共节点,那么必然尾部是”相等的”(准确点说是共用同一条尾部)。通过计算两个链表的长度,来进行对齐。对齐之后,依次访问每个节点。如果节点”相等”,则退出循环,否则返回NULL。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
// 习惯性使用虚拟头结点
ListNode* virtualA = new ListNode;
ListNode* virtualB = new ListNode;
ListNode* curA = new ListNode;
ListNode* curB = new ListNode;
virtualA->next = headA;
virtualB->next = headB;
curA = virtualA;
curB = virtualB;
int lenA = 0;
int lenB = 0;
// 计算链表长度
while(curA->next){
lenA++;
curA = curA->next;
}
while(curB->next){
lenB++;
curB = curB->next;
}
curA = virtualA;
curB = virtualB;
int dst = lenA - lenB;
// 对齐操作
if (dst > 0){
while(dst--){
curA = curA->next;
}
}else if (dst < 0){
dst = -dst;
while(dst--){
curB = curB->next;
}
}
while(curA){
if(curA == curB){ // 注意这里的判断条件是 curA == curB, 而不是 curA->val == curB->val
return curA;
}else{
curA = curA->next;
curB = curB->next;
}
}
return NULL;
}
};
环形链表
使用两个指针,
fast指针每次移动两个位置,slow指针每次移动一个位置,如果有环,则假设在下图紫色位置处相遇。因为fast走过的距离始终是slow的两倍,固有a+b+n(b+c)=2(a+b),化简得a=c+(n-1)(b+c),从起点到入环点的距离恰好等于,相遇点到入环点的距离加上(n-1)圈的环长。也就是说,如果一个点从起点出发,另一个点从相遇点同时出发,那么必定会在入环处相遇。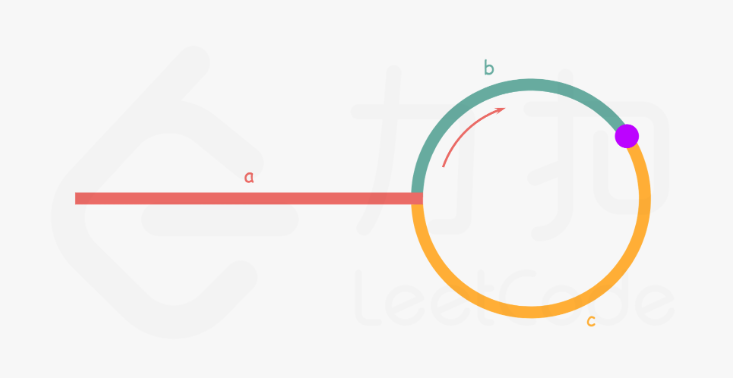
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast){
slow = slow->next;
if(!fast->next){
return NULL;
}
fast = fast->next->next;
if(fast == slow){
ListNode* cur = head;
while(cur != slow){
cur = cur->next;
slow = slow->next;
}
return cur;
}
}
return NULL;
}
};
哈希表
有效的字母异位词
“若
s和t中每个字符出现次数相同,则互为字母异位词”,即将s和t按照a~z的顺序重新排列后,若s==t则互为字母异位词1
2
3
4
5
6
7
8
9
10class Solution {
public:
bool isAnagram(string s, string t) {
if (s.length() != t.length()) return false;
sort(s.begin(),s.end());
sort(t.begin(),t.end());
if (s == t) return true;
return false;
}
};
两个数组的交集
很简单,二傻子都看得懂(如果你觉得我在骂你,那你理解错了;如果你觉得我得是你,那你对了)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_map<int, int> m1;
unordered_map<int, int> m2;
for (auto i: nums1) {
m1[i]++;
}
for (auto i: nums2) {
if (m1[i]) {
m2[i]++;
};
}
vector<int> res;
for (auto i: m2) {
res.push_back(i.first);
}
return res;
}
};
快乐数
采用
set,set是无序且无重复的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool isHappy(int n) {
unordered_set<int> s;
int sum = 0; // 用来存储平方和
while(1){
while(n){
sum += (n%10) * (n%10);
n /= 10;
}
if (sum == 1) return true; // 平方和等于一,则为快乐数
// find会返回一个迭代器,如果找到了,返回的是指向sum的迭代器。否则返回迭代器end()
if (s.find(sum) != s.end()) return false; // sum值在set中已存在,说明已经进入了死循环,不是快乐数
s.insert(sum); // sum值不存在,插入进去
n = sum; // 更新n值
sum = 0; // 注意,要将sum值归零
}
}
};
两数之和
有人相爱,有人夜里开车看海,有人
leetcode第一题都做不出来1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
unordered_map<int, int> m;
for (int i=0;i<nums.size();++i){
auto it = m.find(target - nums[i]);
if (it != m.end()){
res.push_back(i);
res.push_back(it->second);
}else {
m[nums[i]] = i; // 这里不能写m[i]=nums[i],因为find是按照key值查找的,m[key]=val
}
}
return res;
}
};
四数相加 II
两两分组,
unordered_map的key存放第一大组两数之和,value存放该和出现的次数。遍历第二大组,通过查找两数之和的相反数,取其value值。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
int cnt = 0;
int n = nums1.size();
unordered_map<int, int> m;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
m[nums1[i]+nums2[j]]++;
}
}
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
int temp = -(nums3[i]+nums4[j]);
if(m.find(temp) != m.end()){
cnt += m[temp];
}
}
}
return cnt;
}
};
赎金信
首先将两个字符串按
a~z重新排序。采用双指针,如果相等,两个指针同时右移,并且计数器cnt加一;如果不等,将magazine指针右移。结束时,通过比较计数器cnt和ransomNote.size()。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
if(ransomNote.length() > magazine.length()) return false;
sort(ransomNote.begin(),ransomNote.end());
sort(magazine.begin(),magazine.end());
int cnt=0;
for(int i=0,j=0;i<ransomNote.length(),j<magazine.length();){
if(ransomNote[i] == magazine[j]){
cnt++;
i++;
j++;
}else{
j++;
}
}
if(cnt == ransomNote.length()) return true;
return false;
}
};
三数之和
代码分析:记
nums[i]、nums[l]、nums[r]分别为a、b、c,目的是要找到符合a + b + c = 0的组合,且不能重复;第一轮循环中,找到的第一个符合条件的是{-3, 1, 2},left加一之后,找到{-3, 1, 2},很明显,这是个重复的答案,第15行代码就是用来消除结果中b重复的问题;在第二轮循环中,找到第一个符合条件的{-3, 1, 2},很明显,又是个重复答案,第10行代码就是用来消除结果中a重复的问题。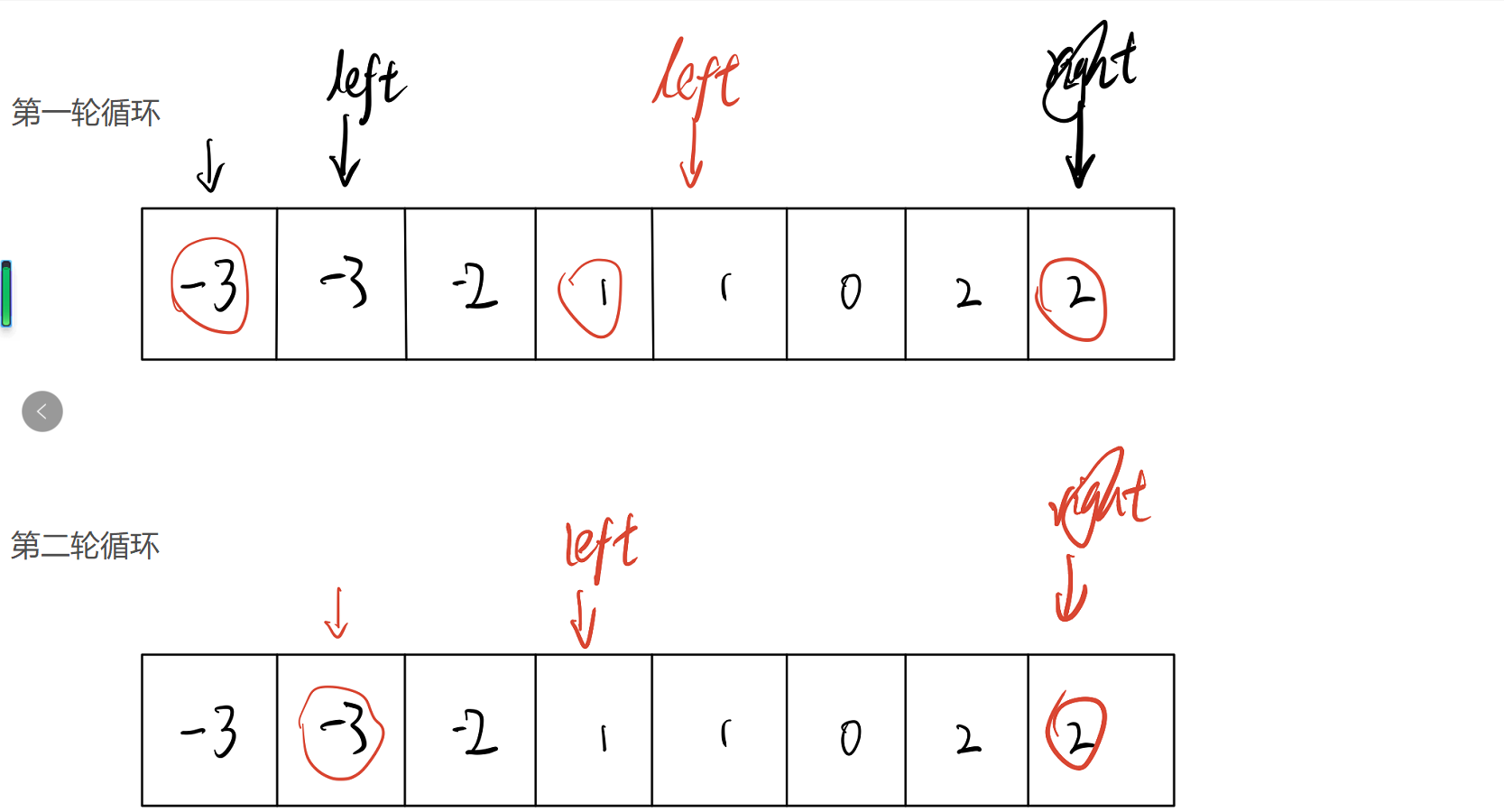
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
if(nums.size()<3) return {};
int n = nums.size();
vector<vector<int>> res;
sort(nums.begin(), nums.end()); // 排序
for (int i = 0; i < n - 2; i++){
if(nums[i] > 0) break; // a如果大于0,表面后续已经没有满足条件的组合了
if(i > 0 && nums[i] == nums[i-1]){ // 消除重复的a
continue;
}
int l = i + 1, r = n - 1;
while(l < r){
if(l>i+1 && nums[l] == nums[l-1]){ // 消除重复的b
l++;
continue;
}
int tmp = 0 - (nums[l] + nums[r]);
if (tmp == nums[i]){
vector<int> em;
em.push_back(nums[i]);
em.push_back(nums[l]);
em.push_back(nums[r]);
res.push_back(em);
l++;
} else if (tmp < nums[i]){
r--;
} else {
l++;
}
}
}
return res;
}
};
四数之和
这道题思路和三数之和一样的,多加一层
for循环。按照上面的思路写的话,测试用例
[1000000000,1000000000,1000000000,1000000000], target = 0,可能会报错,这是因为-10⁹ <= nums[i], target <= 10⁹,而int的范围是-2147483648~2147483647。这也是代码26行和33行写成a+b == t-c-d而不是a+b+c+d == t的原因,如果是a+b+c+d会导致溢出int上限。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
vector<vector<int>> fourSum(vector<int> &nums, int target) {
if (nums.size() < 4) return {};
int n = nums.size();
vector<vector<int>> res;
sort(nums.begin(), nums.end());
for (int i = 0; i < n - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
for (int j = i + 1; j < n - 2; j++) {
if (j > i+1 && nums[j] == nums[j-1]){
continue;
}
int l = j + 1;
int r = n - 1;
while (l < r) {
if (l > j + 1 && nums[l] == nums[l - 1]) {
l++;
continue;
}
// 不要写成nums[l] + nums[r] + nums[i] + nums[j] == target
if (nums[l] + nums[r] == target - nums[i] - nums[j]) {
vector<int> tmp;
tmp.push_back(nums[i]);
tmp.push_back(nums[j]);
tmp.push_back(nums[l]);
tmp.push_back(nums[r]);
res.push_back(tmp);
l++;
} else if (nums[l] + nums[r] < target - nums[i] - nums[j]) {
l++;
} else {
r--;
}
}
}
}
return res;
}
};
字符串
反转字符串
双指针,分别从头尾开始进行交换。
1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
void reverseString(vector<char> &s) {
int n = s.size();
for (int i = 0; i < n / 2; i++) {
swap(s[i], s[n-i-1]);
}
cout << "困难题前唯唯诺诺" << endl;
cout << "简单题我重拳出击" << endl;
}
};
反转字符串 II
for循环,每隔2k个字符,处理一次。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
string reverseStr(string s, int k) {
int n = s.size();
for (int i = 0; i < n; i += 2 * k) {
// 当前剩下的字符串长度小于等于k,直接反转剩下的字符串
if (n - i <= k) {
reverse(s.begin() + i, s.begin() + n);
} else { // 当前剩下的字符串长度大于k,反转前k个字符串
reverse(s.begin() + i, s.begin() + i + k);
}
}
return s;
}
};
替换空格
解法一:用新的空字符串来接收原字符串
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
string replaceSpace(string s) {
string res;
for (auto i: s) {
if (i == ' ') {
res += "%20";
} else {
res += i;
}
}
return res;
}
};
解法二:先统计空格数,然后扩充字符串大小。从后往前,采用双指针,对扩充后的字符串进行修改。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
string replaceSpace(string s) {
int cnt = 0;
int oldSize = s.size();
for(auto i:s){
if(i == ' '){
cnt++;
}
}
s.resize(s.size() + cnt * 2);
int newSize = s.size();
for (int i=oldSize-1,j=newSize-1;i < j;i--,j--){
if(s[i] != ' '){
s[j] = s[i];
}else{
s[j] = '0';
s[j-1] = '2';
s[j-2] = '%';
j -= 2;
}
}
return s;
}
};
颠倒字符串中的单词
解法一:这道题用Go相当简单
1
2
3
4
5
6
7
8
9
10
11
12func reverseWords(s string) string {
res := strings.Split(s, " ") // 以空格为分界线,将原字符串分解为string数组
str := ""
for i := len(res) - 1; i >= 0; i-- {
tmp := strings.Replace(res[i], " ", "", -1) // 去空格操作
if tmp == "" { // 遇到空字符串直接跳过
continue
}
str += tmp + " "
}
return str[:len(str)-1] // 注意返回值,str的最后一个字符为空格
}
解法二:双指针解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79class Solution {
public:
string reverseWords(string s) {
int cnt = 0; // 记录头部空格个数和多余的空格个数
int end = 0; // 记录末尾空格个数
int flag = 0; // 标志位
// 先删除尾部空格
for (int i = s.size() - 1; i >= 0; i--) {
if (s[i] == ' ' && flag == 0) {
end++;
continue;
}
flag = 1;
}
s.erase(s.end() - end, s.end());
flag = 0;
// 删除头部空格和多余的空格
for (int i = 0; i < s.size(); i++) {
// 记录头部空格
if (flag == 0 && s[i] == ' ') {
cnt++;
continue;
}
flag = 1;
// 记录多余的空格
if (i > 0 && s[i - 1] == ' ' && s[i] == ' ') {
cnt++;
}
s[i - cnt] = s[i];
}
s.erase(s.end() - cnt, s.end());
int left = 0;
int right = s.size() - 1;
// 反转字符串
while (left < right) {
swap(s[left], s[right]);
left++;
right--;
}
int slow = 0; // 指向每个单词的头部
int fast = 0; // 指向每个单词的尾部
int tmp = 0;
while (fast < s.size()) {
if (s[fast] != ' ') {
// fast指向最后一个单词的尾部了
if (fast == s.size() - 1){
while (slow < fast) {
swap(s[fast--], s[slow++]);
}
break;
}
fast++;
} else {
fast--; // 注意减一之前指向的是空格,减一之后才指向单词尾部
tmp = fast + 2; // 记录下一个单词的头部
// 反转单词
while (slow < fast) {
swap(s[fast], s[slow]);
slow++;
fast--;
}
// 更新slow和fast,都指向下一个单词的头部
slow = tmp;
fast = tmp;
}
}
return s;
}
};
左旋转字符串
解法一:对原字符串进行扩充,将前n个字符依次拷贝到后n个位置,再将前n个字符删掉
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
string reverseLeftWords(string s, int n) {
int oldSize = s.size();
s.resize(s.size() + n);
for (int i = 0, j = oldSize; i < n; i++, j++) {
s[j] = s[i];
}
s.erase(s.begin(), s.begin() + n);
return s;
}
};
解法二:分别将前n个字符和剩下字符反转一次,最后整体反转一次
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
string reverseLeftWords(string s, int n) {
int left = 0;
int right = n - 1;
while(left < right){
swap(s[left++], s[right--]);
}
left = n;
right = s.size() - 1;
while(left < right){
swap(s[left++], s[right--]);
}
left = 0;
right = s.size() - 1;
while(left < right){
swap(s[left++], s[right--]);
}
return s;
}
};
实现 strStr()
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int strStr(string haystack, string needle) {
if (needle.size() > haystack.size()) return -1;
int i = 0;
int j = 0;
int cnt = 0;
int res = -1;
while (j < needle.size() && i < haystack.size()) {
if (haystack[i + j] == needle[j]) {
j++;
cnt++;
if (cnt == needle.size()) {
res = i;
break;
}
} else {
j = 0;
i++;
cnt = 0;
}
}
return res;
}
};
重复的子字符串
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
vector<int> getNext(string s) {
int n = s.size();
vector<int> next;
next.resize(n);
int j = 0;
next[0] = 0;
for (int i = 1; i < n; i++) {
while (s[j] != s[i] && j > 0) {
j = next[j - 1];
}
if (s[j] == s[i]) {
j++;
}
next[i] = j;
}
return next;
}
bool repeatedSubstringPattern(string s) {
int n = s.size();
if (n == 0) {
return false;
}
auto next = getNext(s);
if (next[n - 1] != 0 && n % (n - next[n - 1]) == 0) {
return true;
}
return false;
}
};
栈与队列
用栈实现队列
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class MyQueue {
public:
stack<int> stIn;
stack<int> stOut;
MyQueue() {
}
void push(int x) {
stIn.push(x);
}
int pop() {
while(stOut.empty()){
while(!stIn.empty()){
stOut.push(stIn.top());
stIn.pop();
}
}
int res = stOut.top();
stOut.pop();
return res;
}
int peek() {
int res = pop();
stOut.push(res);
return res;
}
bool empty() {
return stIn.empty()&&stOut.empty();
}
};
用队列实现栈
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class MyStack {
public:
queue<int> q1;
queue<int> q2;
MyStack() {
}
void push(int x) {
q1.push(x);;
}
int pop() {
while(q1.size() > 1){
q2.push(q1.front());
q1.pop();
}
int res = q1.front();
q1.pop();
q1 = q2;
while(!q2.empty()){
q2.pop();
}
return res;
}
int top() {
int res = pop();
q1.push(res);
return res;
}
bool empty() {
return q1.empty();
}
};
有效的括号
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool isValid(string s) {
stack<int> st;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') st.push(')');
else if (s[i] == '{') st.push('}');
else if (s[i] == '[') st.push(']');
// 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
// 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
else if (st.empty() || st.top() != s[i]) return false;
else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
}
// 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
return st.empty();
}
};
删除字符串中的所有相邻重复项
解法一:使用栈,遍历字符串,栈空或者栈顶元素不等于当前字符时,将当前字符入栈。否则直接出栈。但是超时了…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
string removeDuplicates(string s) {
stack<char> st;
for (auto i: s) {
if (st.empty() || st.top() != i) {
st.push(i);
} else {
st.pop();
}
}
string res = "";
while (!st.empty()) {
res = st.top() + res;
st.pop();
}
return res;
}
};
解法二:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
string removeDuplicates(string s) {
int n = 0;
for (auto c: s) {
if (n == 0 || s[n - 1] != c) {
s[n++] = c;
} else {
n--;
}
}
s.resize(n);
return s;
}
};
逆波兰表达式求值
解法一:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Solution {
public:
int evalRPN(vector<string>& tokens) {
if(tokens.size()==1) return stoi(tokens[0]);
stack<int> st;
int sum = 0;
for (auto i : tokens){
if (i!="+" && i!="-" && i!="*" && i!="/"){
st.push(stoi(i));
}else{
if(i == "+"){
int temp1 = st.top();
st.pop();
int temp2 = st.top();
st.pop();
sum = temp2 + temp1;
st.push(sum);
}
if(i == "-"){
int temp1 = st.top();
st.pop();
int temp2 = st.top();
st.pop();
sum = temp2 - temp1;
st.push(sum);
}
if(i == "*"){
int temp1 = st.top();
st.pop();
int temp2 = st.top();
st.pop();
sum = temp2 * temp1;
st.push(sum);
}
if(i == "/"){
int temp1 = st.top();
st.pop();
int temp2 = st.top();
st.pop();
sum = temp2 / temp1;
st.push(sum);
}
}
}
return sum;
}
};
滑动窗口最大值
解法一:用双端队列来保证窗口里面的值都是从大到小的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
vector<int> maxSlidingWindow(vector<int> &nums, int k) {
vector<int> res;
deque<int> q;
int n = nums.size();
// 首先将前k个放入队列中。每放进一个都跟队尾元素比较,如果大于等于队尾元素,就移除队尾元素
for (int i = 0; i < k; i++) {
while (!q.empty() && nums[q.back()] <= nums[i]) {
q.pop_back();
}
q.push_back(i); // 直到欲放进元素小于队尾元素,将欲放进元素的下标放入队尾
}
// 此时队列中的队头元素一定是此刻窗口中的最大值
res.push_back(nums[q.front()]);
// 滑动窗口,将每个元素都与队尾元素比较
for (int i = k; i < n; i++) {
while (!q.empty() && nums[i] >= nums[q.back()]){
q.pop_back();
}
q.push_back(i);
// 每放入一个新元素,都要处理一下队头元素掉出窗口的情况,要把队头元素移除
while(q.front() + k <= i){
q.pop_front();
}
res.push_back(nums[q.front()]);
}
return res;
}
};来自
leetcode评论区:单调队列真是一种让人感到五味杂陈的数据结构,它的维护过程更是如此…..就拿此题来说,队头最大,往队尾方向单调……有机会站在队头的老大永远心狠手辣,当它从队尾杀进去的时候,如果它发现这里面没一个够自己打的,它会毫无人性地屠城,把原先队里的人头全部丢出去,转身建立起自己的政权,野心勃勃地准备开创一个新的王朝…..这时候,它的人格竟发生了一百八十度大反转,它变成了一位胸怀宽广的慈父!它热情地请那些新来的“小个子”们入住自己的王国……然而,这些小个子似乎天性都是一样的——嫉妒心强,倘若见到比自己还小的居然更早入住王国,它们会心狠手辣地找一个夜晚把它们通通干掉,好让自己享受更大的“蛋糕”;当然,遇到比自己强大的,它们也没辙,乖乖夹起尾巴做人。像这样的暗杀事件每天都在上演,虽然王国里日益笼罩上白色恐怖,但是好在没有后来者强大到足以干翻国王,江山还算能稳住。直到有一天,闯进来了一位真正厉害的角色,就像当年打江山的国王一样,手段狠辣,野心膨胀,于是又是大屠城……历史总是轮回的。
前 K 个高频元素
解法一:使用优先队列(小顶堆),大小为k的小顶堆,每次放入一个元素,当元素个数超过k时,将堆顶元素(即最小值)弹出,最后k个元素就是前k个最大值
1
2
3
4
5
6
7
8
9
10
11
12
13// 优先队列定义:priority_queue<Typename, Container, Functional>
// Typename:入队的数据类型
// Container:实现底层堆的容器,必须是数组容器,如vector,deque
// Functional:比较方式(大顶堆or小顶堆)
//小顶堆 priority_queue <int,vector<int>,greater<int>> pri_que;
//大顶堆 priority_queue <int,vector<int>,less<int>> pri_que;
//默认大顶堆 priority_queue<int> pri_que;代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
class mycomparison {
public:
bool operator()(const pair<int, int> &lhs, const pair<int, int> &rhs) {
return lhs.second > rhs.second;
}
};
vector<int> topKFrequent(vector<int> &nums, int k) {
vector<int> res;
unordered_map<int, int> m;
for (auto i: nums) {
m[i]++;
}
// 定义一个小顶堆
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pri_que;
for (auto i: m) {
pri_que.push(i);
if(pri_que.size() > k){ // 元素大于k个时,弹出堆顶的最小值
pri_que.pop();
}
}
for (int i = 0; i < k; i++) {
res.push_back(pri_que.top().first); // push_back是将元素放在队尾,这里从小到大尾插进去
pri_que.pop();
}
return res;
}
};
二叉树
二叉树基础
定义
1
2
3
4
5
6struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
递归遍历
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
func(root, res);
return res;
}
private:
void func(TreeNode* node, vector<int>& res){
if(node == NULL){
return;
}
res.push_back(node->val);
func(node->left,res);
func(node->right,res);
}
};
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
func(root, res);
return res;
}
void func(TreeNode* node, vector<int>& res){
if (node == NULL) return;
func(node->left, res);
res.push_back(node->val);
func(node->right, res);
}
};
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
func(root, res);
return res;
}
void func(TreeNode* node, vector<int>& res){
if (node == NULL) return;
func(node->left, res);
func(node->right, res);
res.push_back(node->val);
}
};
迭代遍历
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if(root == NULL) return res;
stack<TreeNode*> st;
st.push(root);
while(!st.empty()){
TreeNode* cur = st.top();
res.push_back(cur->val);
st.pop();
if(cur->right) st.push(cur->right);
if(cur->left) st.push(cur->left);
}
return res;
}
};
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if (root == NULL) return res;
TreeNode* cur = root;
stack<TreeNode*> st;
while(cur != NULL || !st.empty()){
if (cur != NULL){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
res.push_back(cur->val);
st.pop();
cur = cur->right;
}
}
return res;
}
};
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
if (root == NULL) return res;
TreeNode* cur = root;
stack<TreeNode*> st;
st.push(cur);
while(!st.empty()){
cur = st.top();
res.push_back(cur->val);
st.pop();
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
reverse(res.begin(), res.end());
return res;
}
};
迭代模板
前序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if (root == NULL) return res;
TreeNode* cur = root;
stack<TreeNode*> st;
st.push(cur);
while(!st.empty()){
cur = st.top();
if(cur != NULL){
st.pop();
// 注意三种迭代的下面四行代码顺序
if(cur->right) st.push(cur->right); // 右
if(cur->left) st.push(cur->left); // 左
st.push(cur); // 中
st.push(NULL);
}else{
st.pop();
cur = st.top();
st.pop();
res.push_back(cur->val);
}
}
return res;
}
};
中序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if (root == NULL) return res;
TreeNode* cur = root;
stack<TreeNode*> st;
st.push(cur);
while(!st.empty()){
cur = st.top();
if(cur != NULL){
st.pop();
if(cur->right) st.push(cur->right); // 右
st.push(cur); // 中
st.push(NULL);
if(cur->left) st.push(cur->left); // 左
}else{
st.pop();
cur = st.top();
st.pop();
res.push_back(cur->val);
}
}
return res;
}
};
后序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if (root == NULL) return res;
TreeNode* cur = root;
stack<TreeNode*> st;
st.push(cur);
while(!st.empty()){
cur = st.top();
if(cur != NULL){
st.pop();
st.push(cur); // 中
st.push(NULL);
if(cur->right) st.push(cur->right); // 右
if(cur->left) st.push(cur->left); // 左
}else{
st.pop();
cur = st.top();
st.pop();
res.push_back(cur->val);
}
}
return res;
}
};
层序遍历
二叉树的层序遍历
1 | class Solution { |
二叉树的层序遍历 II
1 | class Solution { |
二叉树的右视图
1 | class Solution { |
二叉树的层平均值
1 | class Solution { |
N 叉树的层序遍历
1 | class Solution { |
在每个树行中找最大值
1 | class Solution { |
填充每个节点的下一个右侧节点指针
1 | class Solution { |
填充每个节点的下一个右侧节点指针 II
1 | // 跟上面的一模一样。。 |
二叉树的最大深度
1 | class Solution { |
二叉树的最小深度
1 | class Solution { |
翻转二叉树
递归
1
2
3
4
5
6
7
8
9
10class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL) return root;
swap(root->left,root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
迭代
深度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL) return root;
stack<TreeNode*> st;
st.push(root);
TreeNode* cur;
while(!st.empty()){
cur = st.top();
st.pop();
swap(cur->left, cur->right);
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
}
return root;
}
};
广度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root==NULL) return root;
queue<TreeNode*> que;
que.push(root);
TreeNode* cur;
while(!que.empty()){
int size = que.size();
for(int i = 0; i < size; ++i){
cur = que.front();
que.pop();
swap(cur->left,cur->right);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return root;
}
};
模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if (root != NULL) st.push(root);
TreeNode* cur;
while(!st.empty()){
cur = st.top();
if(cur!=NULL){
st.pop();
if(cur->left) st.push(cur->left);
if(cur->right) st.push(cur->right);
st.push(cur);
st.push(NULL);
}else{
st.pop();
cur=st.top();
st.pop();
swap(cur->left, cur->right);
}
}
return root;
}
};
对称二叉树
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root==NULL) return true;
return func(root->left,root->right);
}
bool func(TreeNode* left, TreeNode* right){
// 处理空节点
if(left == NULL && right != NULL) return false;
else if(left != NULL && right == NULL) return false;
else if(left == NULL && right == NULL) return true;
// 处理值不同
else if(left->val != right->val) return false;
// 比较外侧和内侧
bool outside = func(left->left,right->right);
bool inside = func(left->right,right->left);
return outside&&inside;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53// 感觉处理麻烦了,后面有更简单的再更新
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(root==NULL) return true;
queue<TreeNode*> que;
// 处理头结点
if(root->left && root->right){
que.push(root->left);
que.push(root->right);
}else if(!root->left && !root->right){
return true;
}else{
return false;
}
TreeNode* left;
TreeNode* right;
// 头结点有左右子树的情况
while(!que.empty()){
// 如果对称,队列大小必定是偶数
int size = que.size();
if (size % 2 == 1) return false;
for(int i = 0; i < size/2; ++i){
left = que.front();
que.pop();
right = que.front();
que.pop();
if(left->val != right->val) return false;
if(left->left && right->right){
que.push(left->left);
que.push(right->right);
}
if(left->right && right->left){
que.push(left->right);
que.push(right->left);
}
if(left->left && !right->right) return false;
if(!left->left && right->right) return false;
if(left->right && !right->left) return false;
if(!left->right && right->left) return false;
}
}
return true;
}
};
二叉树的最大深度
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL) return 0;
int left = 1 + getDepth(root->left);
int right = 1 + getDepth(root->right);
return max(left, right);
}
int getDepth(TreeNode* node){
if(node == NULL) return 0;
else return 1 + max( getDepth(node->left), getDepth(node->right) );
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int maxDepth(TreeNode* root) {
queue<TreeNode*> que;
if(root != NULL) que.push(root);
int depth = 0;
while(!que.empty()){
depth++;
int size = que.size();
TreeNode* cur;
for(int i = 0; i < size; ++i){
cur = que.front();
que.pop();
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return depth;
}
};
N 叉树的最大深度
递归
1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
int maxDepth(Node* root) {
if (root == NULL) return 0;
int depth = 0;
for(int i = 0; i < root->children.size(); ++i){
depth = max(depth, maxDepth(root->children[i]));
}
return depth + 1;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int maxDepth(Node* root) {
if (root == NULL) return 0;
int depth = 0;
queue<Node*> que;
que.push(root);
Node* cur;
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0; i < size; ++i){
cur = que.front();
que.pop();
for(int i=0;i<cur->children.size();++i){
que.push(cur->children[i]);
}
}
}
return depth;
}
};
二叉树的最小深度
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int minDepth(TreeNode* root) {
if(root == NULL) return 0;
return 1 + getDepth(root);
}
int getDepth(TreeNode* root){
if (root == NULL) return 0;
if(!root->left && !root->right){
return 0;
}else if(root->left && !root->right){
return 1 + getDepth(root->left);
}else if(!root->left && root->right){
return 1 + getDepth(root->right) ;
}else{
return 1 + min(getDepth(root->left), getDepth(root->right));
}
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int minDepth(TreeNode* root) {
int depth = 0;
queue<TreeNode*> que;
if(root != NULL) que.push(root);
while(!que.empty()){
depth++;
int size = que.size();
TreeNode* cur;
for(int i = 0; i < size; ++i){
cur = que.front();
que.pop();
if(cur->left==NULL && cur->right==NULL) return depth;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
}
return depth;
}
};
完全二叉树的节点个数
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int countNodes(TreeNode* root) {
if(root == NULL) return 0;
int left = count(root->left);
int right = count(root->right);
return 1+left+right;
}
int count(TreeNode* node){
if(node == NULL) return 0;
return 1 + count(node->left) + count(node->right);
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int countNodes(TreeNode* root) {
if(root == NULL) return 0;
int res = 0;
queue<TreeNode*> que;
que.push(root);
TreeNode* cur;
while(!que.empty()){
int size = que.size();
res += size;
for(int i = 0; i < size; ++i){
cur = que.front();
que.pop();
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
}
}
return res;
}
};
平衡二叉树
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
bool isBalanced(TreeNode* root) {
if(getHeight(root) == -1) return false;
return true;
}
int getHeight(TreeNode* node){
if (node == NULL) return 0;
int left = getHeight(node->left);
if (left == -1) return -1;
int right = getHeight(node->right);
if (right == -1) return -1;
if ( abs(left-right) > 1 ){
return -1;
}else{
return 1+max(left,right);
}
}
};
迭代
1
// 不好迭,拒绝迭
二叉树的所有路径
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
void findChildren(TreeNode* cur, vector<int>& path, vector<string>& res){
path.push_back(cur->val);
if(!cur->left && !cur->right){
string tmp = "";
for(int i = 0; i < path.size(); ++i){
if(i == path.size()-1){
tmp += to_string(path[i]);
break;
}
tmp += to_string(path[i]);
tmp += "->";
}
res.push_back(tmp);
return;
}
if(cur->left){
findChildren(cur->left, path, res);
path.pop_back();
}
if(cur->right){
findChildren(cur->right, path, res);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
vector<int> path;
if(root == NULL) return res;
findChildren(root, path, res);
return res;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
if (root == NULL) return res;
vector<int> path;
stack<TreeNode *> st;
st.push(root);
while (!st.empty()) {
TreeNode *cur = st.top();
st.pop();
if(cur != NULL){
path.push_back(cur->val);
if(cur->left || cur->right){
st.push(NULL);
if (cur->right) st.push(cur->right);
if (cur->left) st.push(cur->left);
}
if (cur->left==NULL && cur->right==NULL) {
string sPath;
for (int i = 0; i < path.size(); ++i) {
if (i == path.size() - 1) {
sPath += to_string(path[i]);
break;
}
sPath += to_string(path[i]);
sPath += "->";
}
res.push_back(sPath);
path.pop_back();
cur = NULL;
}
}else{
path.pop_back();
}
}
return res;
}
};
左叶子之和
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
void getSum(TreeNode *cur, int &sum) {
if (cur->left && !cur->left->left && !cur->left->right) {
sum += cur->left->val;
}
if (cur->left) getSum(cur->left, sum);
if (cur->right) getSum(cur->right, sum);
}
int sumOfLeftLeaves(TreeNode *root) {
int sum = 0;
getSum(root, sum);
return sum;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int sumOfLeftLeaves(TreeNode *root) {
if(root == NULL) return 0;
int sum = 0;
stack<TreeNode*> st;
st.push(root);
TreeNode* cur;
while(!st.empty()){
cur = st.top();
st.pop();
if (cur->left && !cur->left->left && !cur->left->right) {
sum += cur->left->val;
}
if (cur->right) st.push(cur->right);
if (cur->left) st.push(cur->left);
}
return sum;
}
};
找树左下角的值
递归
1
// 递不动了,不递了
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int findBottomLeftValue(TreeNode *root) {
int res = root->val;
queue<TreeNode *> que;
que.push(root);
TreeNode *cur;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
if (i == 0) res = cur->val;
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
}
}
return res;
}
};
路径总和
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
bool traversal(TreeNode* cur,int count){
if(!cur->left && !cur->right && count==0) return true;
if(!cur->left && !cur->right) return false;
if(cur->left){
count -= cur->left->val;
if(traversal(cur->left, count)) return true;
count += cur->left->val;
}
if(cur->right){
count -= cur->right->val;
if(traversal(cur->right, count)) return true;
count += cur->right->val;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == NULL) return false;
return traversal(root,targetSum-root->val);
}
};
迭代。说一下大致思路:两个栈,
st用来保存先序遍历的顺序,path用来保存已经处理过的结点。每次将结点的儿子结点入栈前,都先将一个NULL结点入栈,NULL结点的用处在于,当我们处理到这个结点的时候,就意味着前面的儿子结点都处理完了,应应当进行回溯了。每从st中取出一个结点,就将该结点放入path中,当取出的结点为NULL时,不放入path中。当处理到叶子结点时,如果不满足条件,则进行回溯。回溯有两步,第一步当然是更改我们的sum值,第二步就是将path的栈顶元素出栈,因为这条路走不通了,当然要换条路.。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
bool hasPathSum(TreeNode *root, int targetSum) {
if (root == NULL) return false;
TreeNode *cur;
TreeNode *pre;
stack<TreeNode *> st; // 先序遍历的顺序入栈
stack<TreeNode *> path; // 保存已经处理过的结点
st.push(root);
int sum = 0;
while (!st.empty()) {
cur = st.top();
st.pop();
if (cur != NULL) {
path.push(cur);
sum += cur->val;
if (!cur->left && !cur->right) {
if (sum == targetSum) return true;
else {
// 回溯
sum -= cur->val;
path.pop();
}
}
if (cur->left || cur->right) {
st.push(NULL); // 标记cur的儿子结点是否处理完毕
if (cur->right) st.push(cur->right);
if (cur->left) st.push(cur->left);
}
} else {
// 处理到NULL结点了,应该进行回溯了
sum -= path.top()->val;
path.pop();
}
}
return false;
}
};
从中序与后序遍历序列构造二叉树
解法一
- 第一步:如果数组大小为零的话,说明是空节点了。
- 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
- 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
- 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
- 第五步:切割后序数组,切成后序左数组和后序右数组
- 第六步:递归处理左区间和右区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
TreeNode* traversal(vector<int>& inorder, vector<int>& postorder){
if (postorder.size() == 0) return NULL;
// 确定父节点
int rootValue = postorder[postorder.size()-1];
TreeNode* root = new TreeNode(rootValue);
if (postorder.size() == 1) return root;
// 根据父节点,在中序遍历中找到该父节点下标
int index;
for(index = 0; index < inorder.size(); ++index){
if(inorder[index] == rootValue) break;
}
// 根据父节点下标,将中序遍历划分为左子树和右子树
vector<int> leftInorder(inorder.begin(), inorder.begin() + index);
vector<int> rightInorder(inorder.begin() + index + 1, inorder.end());
// 中序左/右子树的大小 == 后序左/右子树的大小,根据这一特性来划分后序遍历
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end() - 1);
// 递归处理左区间和右区间
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
从前序与中序遍历序列构造二叉树
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
TreeNode* traversal(vector<int>& preorder, vector<int>& inorder){
if(preorder.size() == 0) return NULL;
int rootValue = preorder[0];
TreeNode* root = new TreeNode(rootValue);
int index;
for (index = 0; index < inorder.size(); ++index){
if (inorder[index] == rootValue) break;
}
vector<int>leftInorder(inorder.begin(), inorder.begin() + index);
vector<int>rightInorder(inorder.begin() + index + 1, inorder.end());
vector<int>leftPreorder(preorder.begin() + 1, preorder.begin() + 1 + leftInorder.size());
vector<int>rightPreorder(preorder.begin() + 1 + leftInorder.size(), preorder.end());
root->left = traversal(leftPreorder, leftInorder);
root->right = traversal(rightPreorder, rightInorder);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (preorder.size() == 0 || inorder.size() == 0) return NULL;
return traversal(preorder, inorder);
}
};
最大二叉树
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
int findMax(vector<int>& nums){
int max = 0;
int index = 0;
for(int i = 0; i < nums.size(); ++i){
if(max < nums[i]){
max = nums[i];
index = i;
}
}
return index;
}
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if(nums.size()==0) return NULL;
int index = findMax(nums);
int rootValue = nums[index];
TreeNode* root = new TreeNode(rootValue);
vector<int> left(nums.begin(), nums.begin() + index);
vector<int> right(nums.begin() + index + 1, nums.end());
root->left = constructMaximumBinaryTree(left);
root->right = constructMaximumBinaryTree(right);
return root;
}
};
合并二叉树
递归
1
2
3
4
5
6
7
8
9
10
11class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root2 == NULL) return root1;
if (root1 == NULL) return root2;
root1->val += root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
TreeNode *mergeTrees(TreeNode *root1, TreeNode *root2) {
if (root2 == NULL) return root1;
if (root1 == NULL) return root2;
queue<TreeNode *> que;
que.push(root1);
que.push(root2);
TreeNode *node1;
TreeNode *node2;
while (!que.empty()) {
node1 = que.front();
que.pop();
node2 = que.front();
que.pop();
node1->val += node2->val;
if (node1->left && node2->left) {
que.push(node1->left);
que.push(node2->left);
}
if (node1->right && node2->right) {
que.push(node1->right);
que.push(node2->right);
}
if (!node1->left && node2->left) {
node1->left = node2->left;
}
if (!node1->right && node2->right) {
node1->right = node2->right;
}
}
return root1;
}
};
二叉搜索树中的搜索
递归
1
2
3
4
5
6
7
8
9class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root == NULL || root->val == val) return root;
if (root->val > val) return searchBST(root->left, val);
if (root->val < val) return searchBST(root->right, val);
return NULL;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if (root == NULL || root->val == val) return root;
queue<TreeNode*> que;
que.push(root);
TreeNode* cur;
while(!que.empty()){
cur = que.front();
que.pop();
if(cur->val == val) return cur;
if(cur->val > val && cur->left) que.push(cur->left);
if(cur->val < val && cur->right) que.push(cur->right);
}
return NULL;
}
};
验证二叉搜索树
递归,先用中序遍历将值保存在数组里,若数组不是递增的,返回
false1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val);
traversal(root->right);
}
bool isValidBST(TreeNode* root) {
traversal(root);
for (int i = 1; i < vec.size(); i++) {
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
TreeNode* pre = NULL;
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root;
bool right = isValidBST(root->right);
return left && right;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
bool isValidBST(TreeNode* root) {
if(root == NULL) return true;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
while(cur != NULL || !st.empty()){
if(cur != NULL){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
st.pop();
if (pre != NULL && pre->val >= cur->val) return false;
pre = cur;
cur = cur->right;
}
}
return true;
}
};
二叉搜索树的最小绝对差
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val);
traversal(root->right);
}
int getMinimumDifference(TreeNode* root) {
traversal(root);
int res = vec[1] - vec[0];
for(int i = 1; i < vec.size(); ++i){
if(vec[i] - vec[i-1] < res) res = vec[i] - vec[i-1];
}
return res;
}
};
递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int res = INT_MAX;
TreeNode* pre = NULL;
void traversal(TreeNode* cur){
if (cur == NULL) return;
traversal(cur->left);
if(pre!=NULL){
res = min(res, cur->val - pre->val);
}
pre = cur;
traversal(cur->right);
}
int getMinimumDifference(TreeNode* root) {
traversal(root);
return res;
}
};
迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int getMinimumDifference(TreeNode* root) {
int res = INT_MAX;
TreeNode* cur = root;
TreeNode* pre =NULL;
stack<TreeNode*> st;
while(cur != NULL || !st.empty()){
if(cur != NULL){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
st.pop();
if(pre != NULL) {
res = min(res, cur->val - pre->val);
}
pre = cur;
cur = cur->right;
}
}
return res;
}
};
二叉搜索树中的众数
解法一,遍历二叉树,用
unordered_map记录次数,全局变量max记录出现的最大次数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
unordered_map<int, int> m;
int max = 0;
void traversal(TreeNode* root){
if (root == NULL) return;
traversal(root->left);
m[root->val]++;
if (max < m[root->val]) max = m[root->val];
traversal(root->right);
}
vector<int> findMode(TreeNode* root) {
traversal(root);
vector<int> res;
for(auto i : m){
if (max == i.second) res.push_back(i.first);
}
return res;
}
};
解法二,中序遍历二叉树,
max记录全局最大次数,count记录当前值出现的次数,如果count = max则将该值放入数组中,如果count > max则清空数组后再放入该值,并且更新max的值。用pre来记录上一个结点。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
int max = 0;
int count = 0;
vector<int> res;
TreeNode* pre = NULL;
void traversal(TreeNode* cur){
if (cur == NULL) return;
traversal(cur->left);
if(pre != NULL && cur->val == pre->val){
++count;
}else{
count = 1;
}
pre = cur;
if (count == max){
res.push_back(cur->val);
}
if (count > max){
max = count;
res.clear();
res.push_back(cur->val);
}
traversal(cur->right);
}
vector<int> findMode(TreeNode* root) {
traversal(root);
return res;
}
};
解法三,迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
vector<int> findMode(TreeNode* root) {
int max = 0;
int count = 0;
vector<int> res;
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL;
while(cur != NULL || !st.empty()){
if (cur != NULL){
st.push(cur);
cur = cur->left;
}else{
cur = st.top();
st.pop();
if(pre != NULL && cur->val == pre->val){
++count;
}else{
count = 1;
}
pre = cur;
if (count == max){
res.push_back(cur->val);
}
if (count > max){
max = count;
res.clear();
res.push_back(cur->val);
}
cur = cur->right;
}
}
return res;
}
};
二叉树的最近公共祖先
解法一
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == p || root == q || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (right != NULL && left != NULL) return root;
if (right == NULL && left != NULL) return left;
if (right != NULL && left == NULL) return right;
else return NULL;
}
};
解法二,遍历每个结点,用哈希表
father存储该结点的值及其父结点。从p结点出发向上寻找,直到根结点,把这一路经过的结点用哈希表path存储起来。再从q结点出发向上寻找,直到找到path中的结点,就是要找的最近公共祖先。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
unordered_map<int, bool> path;
unordered_map<int, TreeNode*> father;
void traversal(TreeNode* cur){
if(cur->left){
father[cur->left->val] = cur;
traversal(cur->left);
}
if(cur->right){
father[cur->right->val] = cur;
traversal(cur->right);
}
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
father[root->val] = NULL;
traversal(root);
while(p != NULL){
path[p->val] = true;
p = father[p->val];
}
while(q != NULL){
if (path[q->val] == true) return q;
q = father[q->val];
}
return NULL;
}
};
二叉搜索树的最近公共祖先
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* cur, TreeNode* p, TreeNode* q) {
if (cur == NULL) return cur;
if (cur->val > p->val && cur->val > q->val) {
return lowestCommonAncestor(cur->left, p, q);
}
if (cur->val < p->val && cur->val < q->val) {
return lowestCommonAncestor(cur->right, p, q);
}
return cur;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* cur;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()){
cur = que.front();
que.pop();
if(cur->val >= min(p->val, q->val) && cur->val <= max(p->val, q->val)) return cur;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
return NULL;
}
};
解法三
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root){
if(root->val > p->val && root->val > q->val){
root = root->left;
}else if(root->val < p->val && root->val < q->val){
root = root->right;
}else return root;
}
return NULL;
}
};
二叉搜索树中的插入操作
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
TreeNode* node = new TreeNode(val);
if (root == NULL) return node;
TreeNode* cur = root;
while(cur){
if(cur->val > val){
if(cur->left != NULL) cur = cur->left;
else{
cur->left = node;
return root;
}
}else if(cur->val < val){
if(cur->right != NULL) cur = cur->right;
else{
cur->right = node;
return root;
}
}
}
return root;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root == NULL) return new TreeNode(val);
if(root->val > val){
if(root->left == NULL){
root->left = new TreeNode(val);
return root;
}else{
insertIntoBST(root->left, val);
}
}
if(root->val < val){
if(root->right == NULL){
root->right = new TreeNode(val);
return root;
}else{
insertIntoBST(root->right, val);
}
}
return root;
}
};
// 可以写得更简洁
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == NULL) {
TreeNode* node = new TreeNode(val);
return node;
}
if (root->val > val) root->left = insertIntoBST(root->left, val);
if (root->val < val) root->right = insertIntoBST(root->right, val);
return root;
}
};
删除二叉搜索树中的节点
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL) return NULL; // 说明没有找到key对应的结点
// 找到了要删除的结点
if(root->val == key){
// 左右孩子都不存在,直接返回NULL,也就是将该结点置空
if(root->left == NULL && root->right == NULL) return NULL;
// 只有一个孩子的情况,直接返回该结点的唯一孩子
else if(root->left != NULL && root->right == NULL){
return root->left;
}
else if(root->left == NULL && root->right != NULL){
return root->right;
}
// 左右孩子都存在,则找到该结点右子树下最左下脚的结点
else{
TreeNode* cur = root->right;
while(cur->left != NULL){
cur = cur->left;
}
cur->left = root->left; // 将该结点的左子树直接接到cur的下面
return root->right; // 返回该结点的右子树
}
}
// 更新左子树或右子树
if(root->val > key) root->left = deleteNode(root->left, key);
if(root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
解法二,普通二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL) return NULL;
if(root->val == key){
if(root->right == NULL){
return root->left;
}
TreeNode* cur = root->right;
while(cur->left){
cur = cur->left;
}
swap(cur->val, root->val);
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
解法三
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
TreeNode* deleteOneNode(TreeNode* node){
if(node == NULL) return NULL;
if(node->right == NULL) return node->left;
TreeNode* cur = node->right;
while(cur->left){
cur = cur->left;
}
cur->left = node->left;
return node->right;
}
TreeNode* deleteNode(TreeNode* root, int key) {
if(root == NULL) return NULL;
TreeNode* cur = root;
TreeNode* pre = NULL;
while(cur){
if(cur->val == key) break;
pre = cur;
if(cur->val > key) cur = cur->left;
else cur = cur->right;
}
if(pre == NULL) return deleteOneNode(root);
if(pre->left && pre->left->val == key) pre->left = deleteOneNode(cur);
if(pre->right && pre->right->val == key) pre->right = deleteOneNode(pre->right);
return root;
}
};
修剪二叉搜索树
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root == NULL) return root;
if(root->val == low) {
root->left = NULL;
root->right = trimBST(root->right, low, high);
}
else if(root->val == high){
root->right = NULL;
root->left = trimBST(root->left, low, high);
}
else if(root->val < low) root = trimBST(root->right, low, high);
else if(root->val > high) root = trimBST(root->left, low, high);
else if(root->val > low && root->val < high){
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
}
return root;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25```
<br>
#### [将有序数组转换为二叉搜索树](https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/)
+ 解法一
```c++
class Solution {
public:
TreeNode* traversal(vector<int>& nums, int left, int right){
if(left > right) return NULL;
int mid = (left + right) / 2;
TreeNode* node = new TreeNode(nums[mid]);
node->left = traversal(nums, left, mid - 1);
node->right = traversal(nums, mid + 1, right);
return node;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};
把二叉搜索树转换为累加树
解法一,其实就是中序遍历然后累加,只不过这里的中序遍历是先遍历右子树
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int sum = 0;
int val = 0;
TreeNode* convertBST(TreeNode* root) {
if(root == NULL) return root;
convertBST(root->right);
val = root->val;
root->val += sum;
sum += val;
convertBST(root->left);
return root;
}
};
回溯
组合
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(int n, int k, int index){
if(path.size() == k){
res.push_back(path);
return;
}
for(int i = index; i <= n; ++i){
path.push_back(i);
backTrack(n, k, i+1);
path.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backTrack(n, k, 1);
return res;
}
};
组合总和 III
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(int n, int k, int index){
if(path.size() == k){
if(n == 0){
res.push_back(path);
}
return;
}
for(int i = index; i <= 9; ++i){
n -= i;
path.push_back(i);
backTrack(n, k, i+1);
path.pop_back();
n +=i;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backTrack(n, k, 1);
return res;
}
};
电话号码的字母组合
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
vector<string> res;
string s;
unordered_map<char, string> phoneMap{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
void backTrack(const string &digits, int index) {
if (s.size() == digits.size()) {
res.push_back(s);
return;
}
char digit = digits[index];
string letter = phoneMap.at(digit);
for (int i = 0; i < letter.size(); ++i) {
s.push_back(letter[i]);
backTrack(digits, index + 1);
s.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if (digits.size() == 0) return res;
backTrack(digits, 0);
return res;
}
};
组合总和
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &candidates, int target, int index) {
if (target < 0) return;
if (target == 0) {
res.push_back(path);
return;
}
for (int i = index; i < candidates.size(); ++i) {
target -= candidates[i];
path.push_back(candidates[i]);
backTrack(candidates, target, i);
target += candidates[i];
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int> &candidates, int target) {
backTrack(candidates, target, 0);
return res;
}
};
组合总和 II
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &candidates, int target, int index, vector<bool> used) {
if (target < 0) return;
if (target == 0) {
res.push_back(path);
return;
}
for (int i = index; i < candidates.size(); ++i) {
// used[i-1]为true说明同一树枝上,已经处理了相同数字
// used[i-1]为false说明同一树层上,已经处理了相同数字
// 只需对同一树层的相同数字跳过
if (i > 0 && !used[i - 1] && candidates[i] == candidates[i - 1]) {
continue;
}
target -= candidates[i];
path.push_back(candidates[i]);
used[i] = true;
backTrack(candidates, target, i + 1, used);
used[i] = false;
path.pop_back();
target += candidates[i];
}
}
vector<vector<int>> combinationSum2(vector<int> &candidates, int target) {
vector<bool> used(candidates.size(), false);
sort(candidates.begin(), candidates.end());
backTrack(candidates, target, 0, used);
return res;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &candidates, int target, int index) {
if (target < 0) return;
if (target == 0) {
res.push_back(path);
return;
}
for (int i = index; i < candidates.size(); ++i) {
if (i > index && candidates[i] == candidates[i - 1]) {
continue;
}
target -= candidates[i];
path.push_back(candidates[i]);
backTrack(candidates, target, i + 1);
path.pop_back();
target += candidates[i];
}
}
vector<vector<int>> combinationSum2(vector<int> &candidates, int target) {
vector<bool> used(candidates.size(), false);
sort(candidates.begin(), candidates.end());
backTrack(candidates, target, 0);
return res;
}
};
分割回文串
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
vector<vector<string>> res;
vector<string> path;
bool isPalindrome(string s, int st, int end) {
while (st < end) {
if (s[st] != s[end]) {
return false;
}
++st;
--end;
}
return true;
}
void backTrack(string s, int index) {
if (index >= s.size()) {
res.push_back(path);
return;
}
for (int i = index; i < s.size(); ++i) {
if (isPalindrome(s, index, i)) {
string str = s.substr(index, i - index + 1);
path.push_back(str);
} else {
continue;
}
backTrack(s, i + 1);
path.pop_back();
}
}
vector<vector<string>> partition(string s) {
backTrack(s, 0);
return res;
}
};
复原 IP 地址
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41class Solution {
public:
vector<string> res;
int pointNum = 0;
bool isValid(string s, int st, int end) {
if (st > end) return false; // 见29行,处理i+2可能越界的问题
if (s[st] == '0' && st != end) return false; // 0开头的多位数不合法
string ip;
for (int i = st; i <= end; ++i) {
ip.push_back(s[i]);
}
if (atoi(ip.c_str()) > 255) return false; // 大于255不合法
return true;
}
void backTrack(string s, int index, int pointNum) {
if (pointNum == 3) {
if (isValid(s, index, s.size() - 1)) {
res.push_back(s);
}
return;
}
for (int i = index; i < s.size(); ++i) {
if (isValid(s, index, i)) {
s.insert(s.begin() + i + 1, '.');
++pointNum;
backTrack(s, i + 2, pointNum); // i+1会将'.'传进去,所以是i+2
--pointNum;
s.erase(s.begin() + i + 1);
} else break;
}
}
vector<string> restoreIpAddresses(string s) {
if (s.size() < 4 || s.size() > 12) return res;
backTrack(s, 0, 0);
return res;
}
};
子集
解法一,在组合题(回溯的第一道题)代码上略作修改
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &nums, int index, int size) {
if (path.size() == size) {
res.push_back(path);
return;
}
for (int i = index; i < nums.size(); ++i) {
path.push_back(nums[i]);
backTrack(nums, i + 1, size);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int> &nums) {
res.push_back({});
for (int i = 1; i <= nums.size(); ++i) {
backTrack(nums, 0, i);
}
return res;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &nums, int index) {
if (index >= nums.size()) {
return;
}
for (int i = index; i < nums.size(); ++i) {
path.push_back(nums[i]);
res.push_back(path);
backTrack(nums, i + 1);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int> &nums) {
res.push_back({});
backTrack(nums, 0);
return res;
}
};
子集 II
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &nums, int index, vector<bool> &used) {
if (index >= nums.size()) {
return;
}
for (int i = index; i < nums.size(); ++i) {
if (i > 0 && !used[i - 1] && nums[i - 1] == nums[i]) {
continue;
}
used[i] = true;
path.push_back(nums[i]);
res.push_back(path);
backTrack(nums, i + 1, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> subsetsWithDup(vector<int> &nums) {
res.push_back({});
sort(nums.begin(), nums.end());
vector<bool> used(nums.size(), false);
backTrack(nums, 0, used);
return res;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
for (int i = startIndex; i < nums.size(); i++) {
if (i > startIndex && nums[i] == nums[i - 1] ) {
continue;
}
path.push_back(nums[i]);
result.push_back(path);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
result.push_back(path);
sort(nums.begin(), nums.end());
backtracking(nums, 0);
return result;
}
};
递增子序列
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &nums, int index) {
if (path.size() > 1) res.push_back(path);
unordered_map<int, bool> used; // 用来记录当前树层出现过的数字
for (int i = index; i < nums.size(); ++i){
if (used[nums[i]]) continue; // 如果在此层,之前出现过该数字,则跳过
if (path.size()>0 && nums[i] < path.back()) continue;
used[nums[i]] = true; // 将此数字标记为true,代表在当前树层出现过
path.push_back(nums[i]);
backTrack(nums, i + 1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int> &nums) {
backTrack(nums, 0);
return res;
}
};
全排列
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
vector<vector<int>> res;
vector<int> path;
int size;
void backTrack(vector<int> &nums) {
if (path.size() == size) {
res.push_back(path);
return;
}
for (int i = 0; i < nums.size(); ++i) {
path.push_back(nums[i]);
vector<int> temp(nums);
temp.erase(temp.begin() + i); // 这里将已选的元素"删掉",避免重复选入
backTrack(temp);
path.pop_back();
}
}
vector<vector<int>> permute(vector<int> &nums) {
size = nums.size();
backTrack(nums);
return res;
}
};
解法二
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int>& nums, unordered_map<int, bool>& used){
if (nums.size() == path.size()){
res.push_back(path);
return;
}
for (int i = 0; i < nums.size(); ++i){
if (used[nums[i]]) continue;
used[nums[i]] = true;
path.push_back(nums[i]);
backTrack(nums, used);
path.pop_back();
used[nums[i]] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
unordered_map<int, bool> used;
backTrack(nums, used);
return res;
}
};
全排列 II
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backTrack(vector<int> &nums, vector<bool> used) {
if (path.size() == nums.size()) {
res.push_back(path);
return;
}
for (int i = 0; i < nums.size(); ++i) {
// 下面说的数值,指数组中大小一样的数字,所以一个数值可能对应多个数字
// 但如果说的是数字,那就特指在当前位置的数字,其他值与其相同的数字不计入其中。
// used[i-1]为true代表同一树枝下,该数值使用过
// used[i-1]为false代表同一树层下,该数值使用过,直接跳过
if (i > 0 && !used[i - 1] && nums[i - 1] == nums[i]) continue;
if (used[i]) continue; // 代表同一树枝下,该数字已经在path中了,不能再次被选
used[i] = true;
path.push_back(nums[i]);
backTrack(nums, used);
used[i] = false;
path.pop_back();
}
}
vector<vector<int>> permuteUnique(vector<int> &nums) {
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end());
backTrack(nums, used);
return res;
}
};
重新安排行程
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42class Solution {
public:
vector<string> path;
// dst代表欲寻找的下一个出发地
bool backTrack(vector<vector<string>> &tickets, string dst, vector<bool> used) {
// 已经使用完所有机票
if (path.size() == tickets.size() + 1) {
return true;
}
for (int i = 0; i < tickets.size(); ++i) {
// 如果最后一张机票的出发地不等于dst,说明这条航线不通,返回false
if (i == tickets.size() - 1 && tickets[i][0] != dst) {
return false;
}
if (tickets[i][0] == dst && !used[i]) {
path.push_back(tickets[i][1]);
used[i] = true;
// 航线不通,回溯
if (!backTrack(tickets, tickets[i][1], used)) {
path.pop_back();
used[i] = false;
}
// 这里还要再判断一次
if (path.size() == tickets.size() + 1) {
return true;
}
}
}
return false;
}
vector<string> findItinerary(vector<vector<string>> &tickets) {
sort(tickets.begin(), tickets.end());
vector<bool> used(tickets.size(), false);
path.push_back("JFK");
backTrack(tickets, "JFK", used);
return path;
}
};
N 皇后
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43class Solution {
public:
vector<vector<string>> res;
bool isValid(int row, int col, vector<string> &table, int n) {
// 检查列
for (int i = 0; i < row; ++i) {
if (table[i][col] == 'Q') return false;
}
// 检查斜左下
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; --j, --i) {
if (table[i][j] == 'Q') return false;
}
// 检查斜右上
for (int i = row - 1, j = col + 1; i >= 0 && j <= n; --i, ++j) {
if (table[i][j] == 'Q') return false;
}
return true;
}
void backTrack(int n, int row, vector<string> &table) {
if (row == n) {
res.push_back(table);
return;
}
for (int col = 0; col < n; ++col) {
if (isValid(row, col, table, n)) {
table[row][col] = 'Q';
backTrack(n, row + 1, table);
table[row][col] = '.';
}
}
}
vector<vector<string>> solveNQueens(int n) {
// 初始化棋盘
vector<string> tables(n, string(n, '.'));
backTrack(n, 0, tables);
return res;
}
};
解数独
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
bool backtracking(vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) {
if (isValid(i, j, k, board)) {
board[i][j] = k;
if (backtracking(board)) return true;
board[i][j] = '.';
}
}
return false;
}
}
return true;
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) {
if (board[row][i] == val || board[i][col] == val) return false;
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) {
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) return false;
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};
贪心
分发饼干
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int findContentChildren(vector<int> &g, vector<int> &s) {
if (s.size() == 0) return 0;
sort(s.begin(), s.end());
sort(g.begin(), g.end());
int number = 0;
int i = s.size() - 1;
int j = g.size() - 1;
while (i >= 0 && j >= 0) {
if (s[i] >= g[j]) {
number++;
i--;
j--;
} else {
j--;
}
}
return number;
}
};
摆动序列
解法一: 摆动序列其实就是找峰值, 大\小于前一个数并且大\小于后一个数就是峰值. 峰值的数量加上2(首尾两个数), 就是摆动序列的长度. 但是要注意如果数组中有连续的重复数, 比如 $3, 1, 1, 3$, 那么此时比较就会失败, 因为对于第一个 $1$ 来讲, 它小于前一个数 $2$, 但是不小于后一个数 $1$, 所以它不是峰值, 同理第二个 $1$ 也如此, 但是这样分析就会导致我们的结果漏掉了一个峰值. 为了避免类似情况发生, 先将数组”去重”.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int wiggleMaxLength(vector<int> &nums) {
int n = nums.size();
vector<int> path;
path.push_back(nums[0]);
// 去掉数组中连续的重复数
for (int i = 1; i < n; ++i) {
if (nums[i] != nums[i - 1]) path.push_back(nums[i]);
}
n = path.size();
if (n <= 2) return n;
int res = 2;
for (int i = 1; i < n - 1; ++i) {
if ((path[i] > path[i - 1] && path[i] > path[i + 1]) || (path[i] < path[i - 1] && path[i] < path[i + 1])) {
res++;
}
}
return res;
}
};
最大子数组和
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int maxSubArray(vector<int> &nums) {
int n = nums.size();
int res = INT_MIN;
int tmp = 0;
for (int i = 0; i < n; ++i) {
tmp += nums[i];
if (res < tmp) {
res = tmp;
}
if (tmp <= 0) tmp = 0;
}
return res;
}
};
买卖股票的最佳时机 II
解法一, 注意股票是可以反复买入卖出的, 也就是说, 只要当天的价格大于前一天的价格, 那么我们就可以卖出
1
2
3
4
5
6
7
8
9
10class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for(int i = 1; i < prices.size(); ++i){
if (prices[i] > prices[i - 1]) res += prices[i] - prices[i-1];
}
return res;
}
};
跳跃游戏
解法一, cover 代表当前能覆盖的最大下标, 当cover大于等于数组的最大下标时, 就代表可以跳至最后一个下标处.
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
bool canJump(vector<int> &nums) {
if (nums.size() == 1) return true;
int cover = 0;
for (int i = 0; i <= cover; ++i) {
cover = max(i + nums[i], cover);
if (cover >= nums.size() - 1) return true;
}
return false;
}
};
跳跃游戏 II
解法一, 每次跳跃都更新可覆盖区域

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int jump(vector<int>& nums) {
int n = nums.size();
int cover = 0;
for (int i = 0; i < n - 1; ++i){
int tmp = cover; // cover是实时更新的,所以每次跳跃时,将cover的值单独保存
for (int j = i; j <= tmp; ++j){
cover = max(j + nums[j], cover);
if (cover >= nums.size() - 1){
return i + 1;
};
}
}
return 0;
}
};
K 次取反后最大化的数组和
解法一, 首先将数组按绝对值大小, 从大到小排序; 遍历, 遇到负值改为正, 并且–k; 遍历结束后, 如果k值为奇数, 说明数组已经全部变为正数, 只需将数组的最后一个数变为负数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
static bool cmp(int a, int b) {
return abs(a) > abs(b);
}
public:
int largestSumAfterKNegations(vector<int> &nums, int k) {
sort(nums.begin(), nums.end(), cmp);
int res = 0;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] < 0 && k > 0) {
nums[i] = -nums[i];
k--;
}
}
if (k % 2 == 1) {
nums[nums.size() - 1] *= -1;
}
for (auto i: nums) res += i;
return res;
}
};
加油站
解法一, curSum 记录从出发站到当前站的油耗量, 如果为负, 则说明出发站选择不对, 出发站位置更新为 i+1, 即当前站点的下一个站, 并且将 curSum 置零; totalSum 记录总的油耗量, 如果为负, 说明怎么都跑不完一周
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int canCompleteCircuit(vector<int> &gas, vector<int> &cost) {
int curSum = 0;
int totalSum = 0;
int start = 0;
for (int i = 0; i < gas.size(); ++i) {
int rest = gas[i] - cost[i];
curSum += rest;
totalSum += rest;
if (curSum < 0) {
start = i + 1;
curSum = 0;
}
}
if (totalSum < 0) return -1;
return start;
}
};
分发糖果
解法一, 第一次遍历从左到右, 将当前值与左侧值比较, 若大于则更新糖果值; 第二次遍历从右到左, 将当前值与右侧值比较, 若大于并且糖果数量也小于等于右侧, 则更新糖果值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int candy(vector<int> &ratings) {
vector<int> candyVec(ratings.size(), 1);
for (int i = 1; i < ratings.size(); ++i) {
if (ratings[i] > ratings[i - 1]) {
candyVec[i] = candyVec[i - 1] + 1;
}
}
for (int i = ratings.size() - 2; i >= 0; --i) {
if (ratings[i] > ratings[i + 1] && candyVec[i] <= candyVec[i + 1]) {
candyVec[i] = candyVec[i + 1] + 1;
}
}
int res = 0;
for (auto i: candyVec) res += i;
return res;
}
};
柠檬水找零
解法一, 注意, 优先找零大额, 再找零小额
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
bool lemonadeChange(vector<int> &bills) {
int five = 0;
int ten = 0;
for (int i = 0; i < bills.size(); ++i) {
if (bills[i] == 5) ++five;
else if (bills[i] == 10) {
if (five >= 1) {
--five;
++ten;
} else return false;
} else {
if (five >= 1 && ten >= 1) {
--five;
--ten;
} else if (five >= 3) {
five -= 3;
} else return false;
}
}
return true;
}
};
根据身高重建队列
解法一
- 第一步: 首先将 people 按身高从矮到高排序
- 第二步: 用 people 中最高的数据去初始化 res
- 第三步: 初始化 used, used[i] 表示 res[i] 在初始化后, 是否更新过值
- 对于 people[i] = [h, k], h 代表身高, k 代表前面正好有 k 个不比他矮的人
- 第四步: 遍历 res, 对于 people[i], 要确保他最后的位置, 前面有 k 个不比他矮的人, 依次比较, 每找到一个身高比 people[i] 高的, 将 k 减一
- 第五步: 当 k 等于0时, 代表已经找到位置, 此时要检查该位置是否已经更新过值, 如果更新过值, 则顺至后一个位置, 如果后一个位置也更新过, 则继续顺位, 直到找到没有更新过值的位置, 找到后, 记得更新 used
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
void find(vector<int> &p, vector<vector<int>> &res, vector<int> &used) {
int height = p[0];
int k = p[1];
for (int i = 0; i < res.size(); ++i) {
if (k == 0 && used[i] == 0) { // 第五步
used[i] = 1;
res[i] = p;
return;
} else {
if (res[i][0] >= height) { // 第四步
--k;
}
}
}
}
vector<vector<int>> reconstructQueue(vector<vector<int>> &people) {
sort(people.begin(), people.end()); // 第一步
vector<vector<int>> res(people.size(), people[people.size() - 1]); // 第二步
vector<int> used(people.size(), 0); // 第三步
for (int i = 0; i < people.size(); ++i) {
find(people[i], res, used);
}
return res;
}
};
解法二, 将 people 按高到矮的顺序排序, 然后依次插入
排序完的 people: [[7,0], [7,1], [6,1], [5,0], [5,2],[4,4]]
插入的过程:
- 插入[7,0]:[[7,0]]
- 插入[7,1]:[[7,0],[7,1]]
- 插入[6,1]:[[7,0],[6,1],[7,1]]
- 插入[5,0]:[[5,0],[7,0],[6,1],[7,1]]
- 插入[5,2]:[[5,0],[7,0],[5,2],[6,1],[7,1]]
- 插入[4,4]:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b) {
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(), cmp);
vector<vector<int>> res;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
res.insert(res.begin() + position, people[i]);
}
return res;
}
};
用最少数量的箭引爆气球
解法一, 两层循环, 暴力求解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int findMinArrowShots(vector<vector<int>> &points) {
sort(points.begin(), points.end());
int res = 0;
vector<int> used(points.size(), 0);
int left;
int right;
for (int i = 0; i < points.size() - 1; ++i) {
if (used[i] == 1) continue;
used[i] = 1;
left = points[i][0];
right = points[i][1];
for (int j = i + 1; j < points.size(); ++j) {
if (used[j] == 1) continue;
if (points[j][0] > right) continue;
left = max(points[j][0], left);
right = min(right, points[j][1]);
used[j] = 1;
}
++res;
}
if (used[points.size() - 1] == 0) ++res;
return res;
}
};
解法二, 每次将当前气球的左边界与当前区间的右边界相比较, 如果大于, 则说明超出了当前区间, 箭数量加一; 否则, 则说明在区间内, 并且更新区间的边界值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int findMinArrowShots(vector<vector<int>> &points) {
sort(points.begin(), points.end());
int res = 1;
for (int i = 1; i < points.size(); ++i) {
if (points[i][0] > points[i - 1][1]) {
++res;
} else {
points[i][1] = min(points[i][1], points[i - 1][1]);
}
}
return res;
}
};
无重叠区间
解法一, 思路和上题差不多, 每次将当前区间的左边界和上一个区间的右边界相比较, 如果左边界小于右边界, 则说明有交集, 注意处理的时候, 要取两个区间, 右边界最小的区间, 这样能保证后续可以容纳更多的区间进去.
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>> &intervals) {
sort(intervals.begin(), intervals.end());
int res = 0;
for (int i = 1; i < intervals.size(); ++i) {
if (intervals[i][0] < intervals[i - 1][1]) {
++res;
intervals[i][1] = min(intervals[i][1], intervals[i - 1][1]);
}
}
return res;
}
};
划分字母区间
解法一, 统计字符串中所有字符的起始和结束位置,记录这些区间, 将区间按左边界从小到大排序, 将区间分组, 各组之间没有交集, 每个组的区间最大起始位置减去最大结束位置, 就是答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
vector<int> partitionLabels(string s) {
vector<int> res;
vector<vector<int>> table(26, vector<int>(2, -1));
for (int i = 0; i < s.size(); ++i) {
int c = s[i] - 97;
if (table[c][0] == -1) {
table[c][0] = i;
table[c][1] = i;
} else {
table[c][1] = i;
}
}
sort(table.begin(), table.end());
int st = 0;
for (int i = 0; i < table.size(); ++i) {
if (table[i][0] != -1) {
st = i;
break;
}
}
int left = table[st][0];
int right = table[st][1];
for (int i = st + 1; i < table.size(); ++i) {
if (table[i][0] > right) {
res.push_back(right - left + 1);
left = table[i][0];
right = table[i][1];
} else {
right = max(right, table[i][1]);
}
if (i == table.size() - 1) {
res.push_back(right - left + 1);
}
}
return res;
}
};
解法二
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
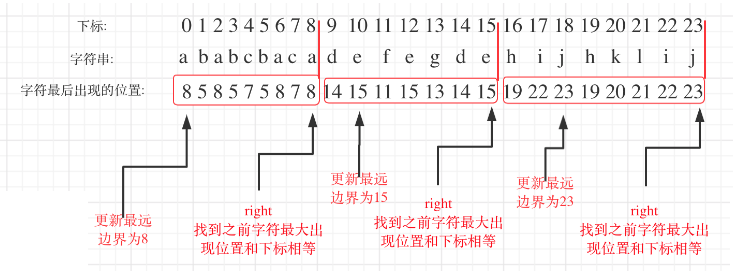
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
vector<int> partitionLabels(string s) {
vector<int> hash(26, 0);
for (int i = 0; i < s.size(); ++i) {
hash[s[i] - 'a'] = i;
}
vector<int> res;
int left = 0;
int right = 0;
for (int i = 0; i < s.size(); ++i) {
right = max(right, hash[s[i] - 'a']);
if (i == right) {
res.push_back(right - left + 1);
left = i + 1;
}
}
return res;
}
};
合并区间
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
vector<vector<int>> merge(vector<vector<int>> &intervals) {
vector<vector<int>> res;
sort(intervals.begin(), intervals.end());
for (int i = 1; i < intervals.size(); ++i) {
if (intervals[i][0] <= intervals[i - 1][1]) {
intervals[i][0] = min(intervals[i][0], intervals[i - 1][0]);
intervals[i][1] = max(intervals[i][1], intervals[i - 1][1]);
} else {
res.push_back(intervals[i - 1]);
}
}
res.push_back(intervals[intervals.size() - 1]); // 记得把最后一个区间加入进去
return res;
}
};
单调递增的数字
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int monotoneIncreasingDigits(int n) {
int i = 1;
int res = n;
while (i <= res / 10) {
int tmp = res / i % 100; // 每次取两个位
i *= 10;
if (tmp / 10 > tmp % 10) { // 比较的高一位大于底一位
res = res / i * i - 1;
/* 例如7654
* 第一次循环7650-1=7649
* 第二次循环7600-1=7599
* 第三次循环7000-1=6999
*/
}
}
return res;
}
};
买卖股票的最佳时机含手续费
解法一
- 情况一:收获利润的这一天并不是收获利润区间里的最后一天(不是真正的卖出,相当于持有股票),所以后面要继续收获利润。
- 情况二:前一天是收获利润区间里的最后一天(相当于真正的卖出了),今天要重新记录最小价格了。
- 情况三:不作操作,保持原有状态(买入,卖出,不买不卖)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int maxProfit(vector<int> &prices, int fee) {
int result = 0;
int minPrice = prices[0]; // 记录最低价格
for (int i = 1; i < prices.size(); i++) {
// 情况二:相当于买入
if (prices[i] < minPrice) minPrice = prices[i];
// 情况三:保持原有状态(因为此时买则不便宜,卖则亏本)
if (prices[i] >= minPrice && prices[i] <= minPrice + fee) {
continue;
}
// 计算利润,可能有多次计算利润,最后一次计算利润才是真正意义的卖出
if (prices[i] > minPrice + fee) {
result += prices[i] - minPrice - fee;
minPrice = prices[i] - fee; // 情况一,这一步很关键
}
}
return result;
}
};
监控二叉树
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int res = 0;
// 0代表有监视器 1代表可观测,但无监视器 2代表不可观测
int dfs(TreeNode* node){
if(node == NULL) return 1;
int left = dfs(node->left);
int right = dfs(node->right);
if(left == 2 || right == 2){
++res;
return 0;
}else if(left == 0 || right == 0){
return 1;
}else{
return 2;
}
}
int minCameraCover(TreeNode* root) {
if(root == NULL) return 0;
if(dfs(root) == 2) ++res;
return res;
}
};
动态规划
斐波那契数
解法一, 递归
1
2
3
4
5
6
7class Solution {
public:
int fib(int n) {
if (n<2) return n;
return fib(n-1) + fib(n-2);
}
};
解法二, 动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int fib(int n) {
if (n<2) return n;
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; ++i){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
解法三, 优化了一下, 只用了三个数组空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int fib(int n) {
if (n<2) return n;
vector<int> dp(3);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; ++i){
dp[2] = dp[1] + dp[0];
dp[0] = dp[1];
dp[1] = dp[2];
}
return dp[2];
}
};
爬楼梯
解法一, 对于第n阶楼梯, 上一步可能是n-1阶或者n-2阶, 所以上到第n阶楼梯的方法等于上到n-1阶和n-2阶楼梯的方法总和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int climbStairs(int n) {
if (n < 3) return n;
vector<int> dp(3);
dp[0] = 1;
dp[1] = 2;
for (int i = 3; i <= n; ++i) {
dp[2] = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = dp[2];
}
return dp[2];
}
};
使用最小花费爬楼梯
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int minCostClimbingStairs(vector<int> &cost) {
if (cost.size() < 3) return min(cost[0], cost[1]);
vector<int> dp(3);
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i <= cost.size(); ++i) {
dp[2] = min(dp[1] + cost[i - 1], dp[0] + cost[i - 2]);
dp[0] = dp[1];
dp[1] = dp[2];
}
return dp[2];
}
};
不同路径
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int uniquePaths(int m, int n) {
if (m == 1 || n == 1) return min(n, m);
vector<vector<int>> dp(m, vector<int>(n, 0));
int i = 0;
while (i < m) dp[i++][0] = 1;
i = 0;
while (i < n) dp[0][i++] = 1;
for (i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
不同路径 II
解法一
- 第一步, 处理第一行, 将0改为1, 直到遇到障碍物
- 第二步, 遇到障碍物之后, 将障碍物及其后续的数均改为0
- 第三步, 按同样的方式处理第一列
- 第四步, 填充dp数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>> &obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
int flag = 0; // 标志位,0代表暂未遇到障碍物
for (int i = 0; i < m; i++) {
if (obstacleGrid[i][0] == 0 && flag == 0) ++obstacleGrid[i][0]; // 第一步
else if (obstacleGrid[i][0] == 1) {
--obstacleGrid[i][0]; // 第二步
flag = 1;
}
}
flag = 0;
// 第三步
for (int j = 1; j < n; j++) {
if (obstacleGrid[0][j] == 0 && flag == 0) ++obstacleGrid[0][j];
else if (obstacleGrid[0][j] == 1) {
--obstacleGrid[0][j];
flag = 1;
}
}
// 第四步
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if (i == 12) {
}
if (obstacleGrid[i][j] == 1) {
obstacleGrid[i][j] = 0;
} else obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
}
}
return obstacleGrid[m - 1][n - 1];
}
};
整数拆分
解法一, 对于正整数 i, 可以拆分成至少两个整数的和, dp[i] 表示最大乘积, 假设拆分出来的第一个正整数为 j, 则有以下两种方案
- 将 i 拆成 j 和 i-j, 且 i-j 不再拆分, 此时乘积为 i*(i-j)
- 将 i 拆成 j 和 i-j, 且 i-j 继续拆分, 此时的乘积为 j*dp[i-j]
1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1);
dp[2] = 1;
for (int i = 3; i <= n ; i++) {
for (int j = 1; j < i - 1; j++) {
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
}
}
return dp[n];
}
};
解法二, 数学方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int integerBreak(int n) {
if (n < 4) return n - 1;
int remainder;
int times;
times = n / 3;
remainder = n % 3;
int res = 1;
for (int i = 1; i < times; ++i) {
res *= 3;
}
if (remainder == 0) return res * 3;
else if (remainder == 1) return res * 4;
else return res * 6;
}
};
不同的二叉搜索树
解法一, 假设有 n 个节点, 以任一节点为根节点, 将剩下的 n-1 个节点分为 i 个节点的左子树和 n-i-1 个节点的右子树, 这种情况下的二叉搜索树一共有: 左子树能构成的所有二叉搜索树数量 * 右子树能构成的所有二叉搜索树数量. i 取不同值(0~n-1), 则 n 个节点可以构成的二叉搜索树数量:
$$dp[n] = \sum_{i=0}^{n}dp[i]*dp[n-i-1]$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
dp[i] += dp[j] * dp[i - j - 1];
}
}
return dp[n];
}
};
分割等和子集
解法一

- dp[i][j] 表示从 [0, i] 这个区间取数, 它们中是否能够选出一些数, 使得他们的和正好等于 j
- 状态转移方程:
- 不选择 nums[i], dp[i][j] = dp[i - 1][j], 其实就是当前这个数大于目标和 j, 那肯定不选择这个数, 那么此时的状态就等于, 不包含这个数(dp[i - 1][..]), 并且目标和也为 j 的状态(dp[…][j]), 即 dp[i - 1][j]
- 选择 nums[i]
- nums[i] == j, dp[i][j] = true, 当前数等于目标和 j, 直接单选这个数就满足了条件, 所以为 true
- nums[i] < j, dp[i][j] = dp[i - 1][j - nums[i]], 当前数小于目标和j, 因为要将这个数放进去, 所以此时的状态就等于, 不包含这个数(dp[i - 1][..]), 并且目标和为 j 减去当前数的状态(dp[…][j - nums[i]]), 即 dp[i - 1][j - nums[i]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
bool canPartition(vector<int> &nums) {
int len = nums.size();
if (len < 2) return false;
int sum = 0;
for (int i = 0; i < len; ++i) {
sum += nums[i];
}
if (sum % 2 == 1) return false;
int target = sum / 2;
vector<vector<bool>> dp(len, vector<bool>(target + 1, false));
for (int i = 0; i < target; ++i) {
if (nums[0] == i) dp[0][i] = true;
}
for (int i = 1; i < len; ++i) {
for (int j = 0; j <= target; ++j) {
if (nums[i] > j) dp[i][j] = dp[i - 1][j];
else if (nums[i] == j) dp[i][j] = true;
else {
dp[i][j] = dp[i - 1][j] | dp[i - 1][j - nums[i]];
}
}
}
return dp[len - 1][target];
}
};
最后一块石头的重量 II
解法一, 转化成01背包, 所有石头的总重量为 sum, 那么我们只需要在所有石头里面, 找出一堆石头其总质量 s1 不大于 sum/2 就行, 那么剩下的所有石头质量 s2 就是 sum-s1, 所以要求的结果就等于 s2 - s1 = sum - (s1 * 2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int lastStoneWeightII(vector<int> &stones) {
int len = stones.size();
if (len < 2) return stones[0];
int sum = 0;
for (auto stone: stones) {
sum += stone;
}
int target = sum / 2;
vector<vector<int>> dp(len, vector<int>(target + 1, 0));
for (int i = 0; i <= target; ++i) {
if (stones[0] <= i) dp[0][i] = stones[0];
}
for (int i = 1; i < len; ++i) {
for (int j = 0; j <= target; ++j) {
if (stones[i] > j) dp[i][j] = dp[i - 1][j];
else {
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
}
}
}
return sum - 2 * dp[len - 1][target];
}
};
目标和
解法一, 问题是给每个整数前添加 $+$ 或者 $-$ 以构成表达式, 使得表达式的结果等于 target. 根据添加符号的不同, 可以将数组分为两个数组, 一个是正数数组, 记和为 N, 一个是负数数组, 记和为 P, 我们记 sum 为整个数组的和, 则有以下推导:
$$N + P = sum$$ $$N - P = target$$ $$N + P + N - P = sum + target$$ $$2N = sum + target$$ $$N = (sum + target) / 2$$
所以问题就转化为, 整个数组能不能找到一个子集, 其和等于 N, 就是01背包问题
dp[i][j] 代表从 nums[0] ~ nums[i] 中取任意数, 其和等于 j 的方法数
初始化
- 第一步对 dp[0][…] 初始化, dp[0][nums[0]] = 1,
- 第二步对 dp[0][0] 初始化, dp[0][0] = 1, 注意, 如果 nums[0][0] == 0, 那么 dp[0][0] = 2, 因为对于0来讲, 在前面加 $+$ 或者 $-$ 都是一样的, 有两种方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
int findTargetSumWays(vector<int> &nums, int target) {
int len = nums.size();
int sum = 0;
for (auto num: nums) {
sum += num;
}
if (abs(sum + target) % 2 != 0) return 0; // sum + target = 2N, 必须为偶数
int N = abs(sum + target) / 2;
vector<vector<int>> dp(len, vector<int>(N + 1, 0));
for (int i = 0; i <= N; ++i) {
if (nums[0] == i) dp[0][i] = 1;
}
if (nums[0] == 0) dp[0][0] = 2;
else dp[0][0] = 1;
for (int i = 1; i < len; ++i) {
for (int j = 0; j <= N; ++j) {
if (nums[i] > j) dp[i][j] = dp[i - 1][j];
else {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
}
}
}
return dp[len - 1][N];
}
};
一和零
解法一, 基础的01背包仅有一个重量限制, 这个问题转化成01背包就是有两个限制m和n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28class Solution {
public:
vector<int> getNums(string &str) {
vector<int> res(2, 0);
for (auto s: str) {
if (s == '0') ++res[0];
else ++res[1];
}
return res;
}
int findMaxForm(vector<string> &strs, int m, int n) {
int len = strs.size();
vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
for (int i = 1; i <= len; ++i) {
vector<int> nums = getNums(strs[i - 1]);
int zero = nums[0];
int one = nums[1];
for (int j = 0; j <= m; ++j) {
for (int k = 0; k <= n; ++k) {
if (zero <= j && one <= k) dp[i][j][k] = max(dp[i - 1][j - zero][k - one] + 1, dp[i - 1][j][k]);
else dp[i][j][k] = dp[i - 1][j][k];
}
}
}
return dp[len][m][n];
}
};
零钱兑换 II
解法一
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int change(int amount, vector<int> &coins) {
int len = coins.size();
vector<int> dp(amount + 1, 0);
dp[0] = 1;
for (int i = 0; i < len; ++i) {
for (int j = coins[i]; j <= amount; ++j) {
dp[j] = dp[j] + dp[j - coins[i]];
}
}
return dp[amount];
}
};
组合总和 Ⅳ
解法一, 求排列数就是外层for遍历背包,内层for循环遍历物品
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int combinationSum4(vector<int> &nums, int target) {
int len = nums.size();
vector<int> dp(target + 1);
dp[0] = 1;
for (int i = 1; i <= target; i++) { // 先背包
for (int j = 0; j < len; ++j) { // 再物品
if (nums[j] <= i && dp[i - nums[j]] < INT_MAX - dp[i]) {
dp[i] = dp[i] + dp[i - nums[j]];
}
}
}
return dp[target];
}
};
零钱兑换
解法一, 求组合数就是外层for循环遍历物品,内层for遍历背包
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int coinChange(vector<int> &coins, int amount) {
int len = coins.size();
if (amount == 0) return 0;
if (len == 1 && coins[0] > amount) return -1;
vector<int> dp(amount + 1, 10001);
dp[0] = 0;
for (int i = 0; i < len; ++i) { // 物品
if (coins[i] > amount) continue; // 如果当前硬币面额大于目标值, 可以直接跳过
for (int j = coins[i]; j <= amount; ++j) { // 背包
dp[j] = min(dp[j], dp[j - coins[i]] + 1);
}
}
return dp[amount] == 10001 ? -1 : dp[amount];
}
};
完全平方数
解法一, 数学方法, 每个正整数均可表示为4个整数的平方和, 所以结果只能在 1 ~ 4 之间
- 如果该整数 $n = 4^k \times (8m + 7)$, 那么该整数只能被表示为四个正整数的平方和, 返回4
- 如果 $n \neq 4^k \times (8m + 7)$
- 如果该整数就是一个完全平方数, 即 $n = a ^ 2$, 返回1
- 如果该整数可以表示为两个整数的平方和, 即 $n = a ^ 2 + b ^ 2$ , 返回2
- 否则返回3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
bool isPerfectNumber(int n) {
int x = sqrt(n);
return x * x == n;
}
bool check(int n) {
while (n % 4 == 0) {
n /= 4;
}
return n % 8 == 7;
}
int numSquares(int n) {
if (isPerfectNumber(n)) return 1;
else if (check(n)) return 4;
else {
for (int i = 1; i * i <= n; ++i) {
int j = n - i * i;
if (isPerfectNumber(j)) return 2;
}
return 3;
}
}
};
单词拆分
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool wordBreak(string s, vector<string> &wordDict) {
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) { // 遍历背包
for (int j = 0; j < i; j++) { // 遍历物品
string word = s.substr(j, i - j); // substr(起始位置,截取的个数)
auto flag = find(wordDict.begin(), wordDict.end(), word);
if (flag != wordDict.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
打家劫舍
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
int rob(vector<int> &nums) {
int len = nums.size();
if (len == 1) return nums[0];
if (len == 2) return max(nums[0], nums[1]);
vector<int> dp(len, 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < len; ++i) {
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[len - 1];
}
};
打家劫舍 II
解法一, 如果打劫第一家人, 那么最后一家人就不能打劫, 如果不打劫第一家人, 那么最后一家就可以打劫
问题转化成, 打劫 0
n-2 号人家和打劫 1n-1 号人家两种方案1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
int rob(vector<int> &nums) {
int len = nums.size();
if (len == 1) return nums[0];
if (len == 2) return max(nums[0], nums[1]);
if (len == 3) return max(max(nums[0], nums[1]), nums[2]);
vector<int> dp(len, 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
// 一共 n 家人, 0 ~ n-1
// 打劫 0 ~ n-2
for (int i = 2; i < len - 1; ++i) {
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
}
int total = dp[len - 2];
// 打劫 1 ~ n-1
dp[0] = 0;
dp[1] = nums[1];
for (int i = 2; i <= len - 1; ++i) {
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
}
return max(dp[len - 1], total);
}
};
打家劫舍 III
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
unordered_map<TreeNode *, int> sums;
int robTree(TreeNode *node) {
if (node == NULL) return 0;
if (sums.count(node)) return sums[node];
int left = 0;
int right = 0;
if (node->left) {
left = robTree(node->left->left) + robTree(node->left->right);
}
if (node->right) {
right = robTree(node->right->left) + robTree(node->right->right);
}
int self = left + right + node->val;
int children = robTree(node->left) + robTree(node->right);
sums[node] = max(self, children);
return sums[node];
}
int rob(TreeNode *root) {
return robTree(root);
}
};
买卖股票的最佳时机
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int maxProfit(vector<int> &prices) {
int len = prices.size();
if (len == 1) return 0;
int Min = prices[0];
vector<int> dp(len, 0);
for (int i = 1; i < len; ++i) {
dp[i] = max(dp[i - 1], prices[i] - Min);
Min = min(prices[i], Min);
}
return dp[len - 1];
}
};
买卖股票的最佳时机 II
解法一
1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
if (len == 1) return 0;
vector<int> dp(len, 0);
for (int i = 1; i < len; ++i) {
dp[i] = max(dp[i - 1], dp[i - 1] + prices[i] - prices[i - 1]);
}
return dp[len - 1];
}
};
买卖股票的最佳时机 III
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxProfit(vector<int> &prices) {
if (prices.size() == 1) return 0;
int buy1 = -prices[0];
int sell1 = 0;
int buy2 = -prices[0];
int sell2 = 0;
for (int i = 1; i < prices.size(); ++i) {
buy1 = max(buy1, -prices[i]);
sell1 = max(sell1, buy1 + prices[i]);
buy2 = max(buy2, sell1 - prices[i]);
sell2 = max(sell2, buy2 + prices[i]);
}
return sell2;
}
};
买卖股票的最佳时机 IV
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int maxProfit(int k, vector<int> &prices) {
vector<vector<int>> dp(k, vector<int>(2, 0));
for (int i = 0; i < k; ++i) {
dp[i][0] = -prices[0];
}
for (int i = 1; i < prices.size(); ++i) {
for (int j = 0; j < k; ++j) {
if (j == 0) {
dp[j][0] = max(dp[j][0], -prices[i]);
dp[j][1] = max(dp[j][1], dp[j][0] + prices[i]);
continue;
}
dp[j][0] = max(dp[j][0], dp[j - 1][1] - prices[i]);
dp[j][1] = max(dp[j][1], dp[j][0] + prices[i]);
}
}
return dp[k - 1][1];
}
};
最佳买卖股票时机含冷冻期
解法一,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22// sell[i] 前i天最后一个操作为卖出 = max(buy[i]+prices[i], sell[i-1])
// buy[i] 前i天最后一个操作为买入 = max(cool[i-1]-prices[i], buy[i-1])
// cool[i] 前i天最后一个操作为冷冻期 = sell[i-1]
class Solution {
public:
int maxProfit(vector<int> &prices) {
int len = prices.size();
if (len < 2) return 0;
vector<int> sell(len, 0);
vector<int> buy(len, 0);
vector<int> cool(len, 0);
buy[0] = -prices[0];
for (int i = 1; i < len; ++i) {
buy[i] = max(cool[i - 1] - prices[i], buy[i - 1]);
cool[i] = sell[i - 1];
sell[i] = max(buy[i - 1] + prices[i], sell[i - 1]);
}
return sell[len - 1];
}
};
买卖股票的最佳时机含手续费
解法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int maxProfit(vector<int> &prices, int fee) {
int len = prices.size();
if (len < 2) return 0;
vector<vector<int>> dp(len, vector<int>(2, 0));
// dp[i][0] 代表当天交易完, 手里没有股票
// dp[i][1] 代表当天交易完, 手里有股票
dp[0][1] = -prices[0];
for (int i = 1; i < len; ++i) {
// 今天交易了,也就是把今天的股票卖了出去; 今天没交易,状态跟昨天一样
dp[i][0] = max(dp[i - 1][1] + prices[i] - fee, dp[i - 1][0]);
// 今天交易了,也就是买了今天的股票; 今天没交易,状态跟昨天一样
dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
}
return dp[len - 1][0];
}
};
最长递增子序列
解法一
```c++
持续更新…
- 本文作者: 谷安
- 本文链接: http://example.com/2022/04/11/leetcode-Note/
- 版权声明: 转载请注明出处



